Trojrozměrný prostor - Three-dimensional space - Wikipedia
Tento článek obsahuje seznam obecných Reference, ale zůstává z velké části neověřený, protože postrádá dostatečné odpovídající vložené citace. (Dubna 2016) (Zjistěte, jak a kdy odstranit tuto zprávu šablony) |
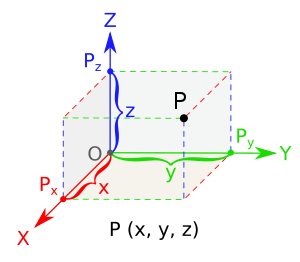
Trojrozměrný prostor (taky: 3-prostor nebo zřídka trojrozměrný prostor) je geometrické nastavení, ve kterém tři hodnoty (tzv parametry ) jsou určeny k určení polohy prvku (tj. směřovat ). Toto je neformální význam tohoto pojmu dimenze.
v fyzika a matematika, a sekvence z n čísla lze chápat jako místo v n-rozměrný prostor. Když n = 3se nazývá sada všech takových umístění trojrozměrný Euklidovský prostor (nebo jednoduše euklidovský prostor, když je kontext jasný). Běžně je reprezentován symbolem ℝ3.[1][2] To slouží jako tříparametrový model fyzické vesmír (tj. prostorová část, bez ohledu na čas), ve které je vše známé hmota existuje. I když tento prostor zůstává nejpřesvědčivějším a nejužitečnějším způsobem, jak modelovat svět, jak je zažíván,[3] je to jen jeden příklad velké škály prostorů ve třech dimenzích 3 rozdělovače. V tomto klasickém příkladu, když tři hodnoty odkazují na měření v různých směrech (souřadnice ) lze zvolit libovolné tři směry, pokud vektory v těchto směrech ne všichni leží ve stejném 2-prostor (letadlo ). Dále v tomto případě mohou být tyto tři hodnoty označeny libovolnou kombinací tří vybraných z výrazů šířka, výška, hloubka, a délka.
V euklidovské geometrii
Souřadnicové systémy
V matematice analytická geometrie (také nazývaný kartézská geometrie) popisuje každý bod v trojrozměrném prostoru pomocí tří souřadnic. Tři souřadnicové osy jsou uvedeny, každý kolmý na další dva v původ, bod, ve kterém se kříží. Obvykle jsou označeny X, y, a z. Ve vztahu k těmto osám je poloha libovolného bodu v trojrozměrném prostoru dána uspořádanou trojicí reálná čísla, každé číslo udává vzdálenost daného bodu od původ měřeno podél dané osy, která se rovná vzdálenosti tohoto bodu od roviny určené dalšími dvěma osami.[4]
Mezi další populární metody popisu polohy bodu v trojrozměrném prostoru patří válcové souřadnice a sférické souřadnice, i když existuje nekonečné množství možných metod. Více viz Euklidovský prostor.
Níže jsou obrázky výše zmíněných systémů.
Čáry a letadla
Dva odlišné body vždy určují (rovný) čára. Tři odlišné body jsou buď kolineární nebo určit jedinečnou rovinu. Na druhou stranu, čtyři odlišné body mohou být buď kolineární, koplanární, nebo určit celý prostor.
Dvě odlišné linie se mohou protínat, být paralelní nebo být překroutit. Dvě rovnoběžné čáry, nebo dvě protínající se čáry, leží v jedinečné rovině, takže šikmé čáry jsou čáry, které se nesetkávají a neleží ve společné rovině.
Dvě odlišné roviny se mohou setkat ve společné linii nebo jsou rovnoběžné (tj. Nesetkat se). Tři odlišné roviny, z nichž žádná dvojice není paralelní, se mohou setkat ve společné linii, setkat se v jedinečném společném bodě nebo nemají žádný společný bod. V posledním případě jsou tři průsečíky každé dvojice rovin vzájemně rovnoběžné.
Přímka může ležet v dané rovině, protínat ji v jedinečném bodě nebo být rovnoběžná s rovinou. V posledním případě budou v rovině čáry, které jsou rovnoběžné s danou čarou.
A nadrovina je podprostor o jednu dimenzi menší než dimenze celého prostoru. Hyperplány trojrozměrného prostoru jsou dvourozměrné podprostory, tj. Roviny. Z hlediska kartézských souřadnic splňují body nadroviny jediný lineární rovnice, takže roviny v tomto 3 prostoru jsou popsány lineárními rovnicemi. Přímku lze popsat dvojicí nezávislých lineárních rovnic - každá představuje rovinu, která má tuto přímku jako společný průsečík.
Varignonova věta uvádí, že středy libovolného čtyřúhelníku v ℝ3 tvoří a rovnoběžník, a proto jsou koplanární.
Koule a koule

A koule ve 3-prostoru (také nazývaný a 2 koule protože se jedná o dvourozměrný objekt) sestává ze sady všech bodů ve 3prostoru v pevné vzdálenosti r z centrálního bodu P. Těleso uzavřené koulí se nazývá a míč (nebo přesněji a 3 míčky). Objem míče je dán vztahem
- .
Další typ koule vychází ze 4-koule, jejíž trojrozměrný povrch je 3 koule: body ve stejné vzdálenosti od počátku euklidovského prostoru ℝ4. Pokud má bod souřadnice, P(X, y, z, w), pak X2 + y2 + z2 + w2 = 1 charakterizuje ty body na jednotce 3-koule se středem na počátku.
Polytopes
Ve třech rozměrech existuje devět pravidelných polytopů: pět konvexních Platonické pevné látky a čtyři nekonvexní Kepler-Poinsotův mnohostěn.
| Třída | Platonické pevné látky | Kepler-Poinsotův mnohostěn | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Symetrie | Td | Óh | Jáh | ||||||
| Skupina coxeterů | A3, [3,3] | B3, [4,3] | H3, [5,3] | ||||||
| Objednat | 24 | 48 | 120 | ||||||
| Pravidelný mnohostěn | {3,3} |  {4,3} |  {3,4} |  {5,3} | {3,5} |  {5/2,5} |  {5,5/2} | {5/2,3} |  {3,5/2} |
Revoluční povrchy
A povrch generované otáčením roviny křivka o pevné linii v její rovině jako ose se nazývá a povrch otáčení. Rovinná křivka se nazývá generatrix povrchu. Část plochy, vytvořená protínáním plochy s rovinou, která je kolmá (kolmá) na osu, je kruh.
Jednoduché příklady nastávají, když je generatrix čára. Pokud čára generatrix protíná osu, je rotační plocha pravá kruhová kužel s vrcholem (průsečíkem) průsečík. Pokud jsou však generatrix a osa rovnoběžné, pak je rotační plocha kruhová válec.
Quadric plochy
Analogicky s kuželovité úseky, množina bodů, jejichž kartézské souřadnice splňují obecnou rovnici druhého stupně, jmenovitě,
kde A, B, C, F, G, H, J, K., L a M jsou skutečná čísla a ne všechna A, B, C, F, G a H jsou nula, nazývá se a kvadrický povrch.[5]
Existuje šest typů nedegenerovaný kvadrické povrchy:
- Elipsoid
- Hyperboloid jednoho listu
- Hyperboloid dvou listů
- Eliptický kužel
- Eliptický paraboloid
- Hyperbolický paraboloid
Degenerované kvadrické povrchy jsou prázdná množina, jediný bod, jedna čára, jedna rovina, dvojice rovin nebo kvadratický válec (povrch skládající se z nedegenerovaného kuželovitého řezu v rovině π a všechny řádky ℝ3 přes ten kuželovitý tvar, který je normální π).[5] Eliptické kužele jsou někdy také považovány za degenerované kvadrické povrchy.
Jak hyperboloid jednoho listu, tak hyperbolický paraboloid jsou ovládané povrchy, což znamená, že mohou být vytvořeny z rodiny přímek. Ve skutečnosti má každá dvě rodiny generujících linií, členové každé rodiny jsou disjunktní a každý člen protíná jednu rodinu, až na jednu výjimku, každý člen druhé rodiny.[6] Každá rodina se nazývá a regulus.
V lineární algebře
Další způsob prohlížení trojrozměrného prostoru se nachází v lineární algebra, kde je zásadní myšlenka nezávislosti. Prostor má tři rozměry, protože délka a krabice je nezávislý na jeho šířce nebo šířce. V technickém jazyce lineární algebry je prostor trojrozměrný, protože každý bod v prostoru lze popsat lineární kombinací tří nezávislých vektory.
Tečkovaný produkt, úhel a délka
Vektor lze zobrazit jako šipka. Velikost vektoru je jeho délka a jeho směr je směr, na který ukazuje šipka. Vektor v ℝ3 může být reprezentován uspořádanou trojicí reálných čísel. Tato čísla se nazývají komponenty vektoru.
Tečkový produkt dvou vektorů A = [A1, A2, A3] a B = [B1, B2, B3] je definován jako:[7]
Velikost vektoru A je označen ||A||. Tečkový produkt vektoru A = [A1, A2, A3] sama se sebou je
který dává
vzorec pro Euklidovská délka vektoru.
Bez odkazu na složky vektorů, bodový produkt dvou nenulových euklidovských vektorů A a B je dána[8]
kde θ je úhel mezi A a B.
Křížový produkt
The křížový produkt nebo vektorový produkt je binární operace na dva vektory v trojrozměrném prostor a je označen symbolem ×. Křížový produkt A × b vektorů A a b je vektor, který je kolmý oběma a proto normální do letadla, které je obsahuje. Má mnoho aplikací v matematice, fyzika, a inženýrství.
Prostor a produkt tvoří algebra nad polem, což není ani jedno, ani druhé komutativní ani asociativní, ale je Lež algebra přičemž křížovým produktem je Lieova závorka.
Jeden může dovnitř n rozměry berou produkt n − 1 vektory k vytvoření vektoru kolmého na všechny z nich. Pokud je však produkt omezen na netriviální binární produkty s vektorovými výsledky, existuje pouze ve třech a sedm rozměrů.[9]

V počtu
Přechod, divergence a zvlnění
V pravoúhlém souřadnicovém systému je gradient dán vztahem
Divergence a průběžně diferencovatelné vektorové pole F = U i + PROTI j + Ž k se rovná skalární -hodnota funkce:
Rozšířeno Kartézské souřadnice (vidět Del ve válcových a sférických souřadnicích pro sférický a válcovitý reprezentace souřadnic), zvlnění ∇ × F je pro F složen z [FX, Fy, Fz]:
kde i, j, a k jsou jednotkové vektory pro X-, y-, a z-axes, resp. Toto se rozšiřuje následovně:[10]
Lineární integrály, povrchové integrály a objemové integrály
Pro některé skalární pole F : U ⊆ Rn → R, čára integrální podél a po částech hladký křivka C ⊂ U je definován jako
kde r: [a, b] → C je libovolný bijektivní parametrizace křivky C takhle r(A) a r(b) uveďte koncové body C a .
Pro vektorové pole F : U ⊆ Rn → Rn, čára integrální podél a po částech hladký křivka C ⊂ U, ve směru r, je definován jako
kde je Tečkovaný produkt a r: [a, b] → C je bijektivní parametrizace křivky C takhle r(A) a r(b) uveďte koncové body C.
A povrchový integrál je zobecněním více integrálů k integraci povrchy. Lze to považovat za dvojitý integrál obdoba linka integrální. Abychom našli explicitní vzorec pro plošný integrál, musíme parametrizovat povrch zájmu, Szvážením systému křivočaré souřadnice na S, jako zeměpisná šířka a zeměpisná délka na koule. Nechť je taková parametrizace X(s, t), kde (s, t) se v některých regionech liší T v letadlo. Potom je povrchový integrál dán vztahem
kde výraz mezi pruhy na pravé straně je velikost z křížový produkt z částečné derivace z X(s, t), a je znám jako povrch živel. Vzhledem k tomu, vektorové pole proti na S, to je funkce, která je každému přiřazena X v S vektor proti(X), plošný integrál lze definovat po komponentách podle definice povrchového integrálu skalárního pole; výsledkem je vektor.
A objemový integrál odkazuje na integrální přes 3-dimenzionální doména.
Může to také znamenat a trojitý integrál v rámci regionu D v R3 a funkce a obvykle se píše jako:
Základní věta lineárních integrálů
The základní teorém lineárních integrálů, říká, že a linka integrální přes a spád pole lze vyhodnotit vyhodnocením původního skalárního pole v koncových bodech křivky.
Nechat . Pak
Stokesova věta
Stokesova věta se týká povrchový integrál z kučera a vektorové pole F přes povrch Σ v euklidovském tříprostoru k linka integrální vektorového pole přes jeho hranici ∂Σ:
Věta o divergenci
Předpokládat PROTI je podmnožinou (v případě n = 3, PROTI představuje svazek ve 3D prostoru), který je kompaktní a má po částech hladká hranice S (označeno také ∂PROTI = S ). Li F je spojitě diferencovatelné vektorové pole definované na sousedství PROTI, pak věta o divergenci říká:[11]
Levá strana je a objemový integrál přes hlasitost PROTI, pravá strana je povrchový integrál přes hranici svazku PROTI. Uzavřené potrubí ∂PROTI je obecně hranice PROTI orientováno směrem ven normály, a n je ven směřující jednotka normální pole hranice ∂PROTI. (dS lze použít jako zkratku pro ndS.)
V topologii

Trojrozměrný prostor má řadu topologických vlastností, které jej odlišují od prostorů jiných čísel dimenzí. Například pro svázání a. Jsou zapotřebí alespoň tři rozměry uzel v provázku.[12]
v diferenciální geometrie obecné trojrozměrné prostory jsou 3 rozdělovače, které se místně podobají .
V konečné geometrii
Lze otestovat mnoho nápadů dimenze konečná geometrie. Nejjednodušší instance je PG (3,2), který má Fano letadla jako jeho 2-dimenzionální podprostory. Je to instance Galoisova geometrie, studie o projektivní geometrie použitím konečná pole. Pro každé pole Galois GF (q), tady je projektivní prostor PG (3,q) tří dimenzí. Například jakékoli tři šikmé čáry v PG (3,q) jsou obsaženy přesně v jednom regulus.[13]
Viz také
- Dimenzionální analýza
- Vzdálenost od bodu k rovině
- Čtyřrozměrný prostor
- Šikmé čáry § Vzdálenost
- Trojrozměrný graf
- Dvourozměrný prostor
Poznámky
- ^ „Kompendium matematických symbolů“. Matematický trezor. 2020-03-01. Citováno 2020-08-12.
- ^ „Euklidovský prostor - encyklopedie matematiky“. encyclopediaofmath.org. Citováno 2020-08-12.
- ^ "Euklidovský prostor | geometrie". Encyklopedie Britannica. Citováno 2020-08-12.
- ^ Hughes-Hallett, Deborah; McCallum, William G .; Gleason, Andrew M. (2013). Calculus: Single and Multivariable (6. vyd.). John Wiley. ISBN 978-0470-88861-2.
- ^ A b Brannan, Esplen & Gray 1999, str. 34–5
- ^ Brannan, Esplen & Gray 1999, str. 41–2
- ^ Anton 1994, str. 133
- ^ Anton 1994, str. 131
- ^ WS Massey (1983). "Křížové produkty vektorů ve vyšších dimenzionálních euklidovských prostorech". Americký matematický měsíčník. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537.
Pokud jeden vyžaduje pouze tři základní vlastnosti křížového produktu ... ukáže se, že křížový produkt vektorů existuje pouze v 3-dimenzionálním a 7-dimenzionálním euklidovském prostoru.
CS1 maint: ref = harv (odkaz) - ^ Arfken, str. 43.
- ^ M. R. Spiegel; S. Lipschutz; D. Spellman (2009). Vektorová analýza. Schaum's Outlines (2. vyd.). USA: McGraw Hill. ISBN 978-0-07-161545-7.
- ^ Rolfsen, Dale (1976). Uzly a odkazy. Berkeley, Kalifornie: Publikovat nebo zahynout. ISBN 0-914098-16-0.
- ^ Albrecht Beutelspacher & Ute Rosenbaum (1998) Projektivní geometrie, strana 72, Cambridge University Press ISBN 0-521-48277-1
Reference
- Anton, Howard (1994), Elementární lineární algebra (7. vydání), John Wiley & Sons, ISBN 978-0-471-58742-2
- Arfken, George B. a Hans J. Weber. Matematické metody pro fyziky, Academic Press; 6. vydání (21. června 2005). ISBN 978-0-12-059876-2.
- Brannan, David A .; Esplen, Matthew F .; Gray, Jeremy J. (1999), Geometrie, Cambridge University Press, ISBN 978-0-521-59787-6
externí odkazy
 Slovníková definice trojrozměrný na Wikislovníku
Slovníková definice trojrozměrný na Wikislovníku- Weisstein, Eric W. „Čtyřrozměrná geometrie“. MathWorld.
- Elementární lineární algebra - Kapitola 8: Trojrozměrná geometrie Keith Matthews z University of Queensland, 1991





















![varphi left ( mathbf {q} right) - varphi left ( mathbf {p} right) = int _ { gamma [ mathbf {p}, , mathbf {q}]} nabla varphi ( mathbf {r}) cdot d mathbf {r}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/b27cdd0377931a70cbb0635e37781a42e7fe33f9)






