Sekvence - Sequence
v matematika, a sekvence je vyjmenovaná kolekce objektů, ve kterých je povoleno opakování a objednat záležitosti. Jako soubor, obsahuje členů (také zvaný elementynebo podmínky). Počet prvků (možná nekonečných) se nazývá délka sekvence. Na rozdíl od sady se stejné prvky mohou objevit několikrát na různých pozicích v pořadí a na rozdíl od sady záleží na pořadí. Formálně lze sekvenci definovat jako a funkce jehož doménou je buď soubor přirozená čísla (pro nekonečné sekvence) nebo množinu prvního n přirozená čísla (pro posloupnost konečné délky n).
Například (M, A, R, Y) je posloupnost písmen s prvním písmenem „M“ a posledním „Y“. Tato sekvence se liší od (A, R, M, Y). Sekvence (1, 1, 2, 3, 5, 8), která obsahuje číslo 1 na dvou různých pozicích, je také platnou sekvencí. Sekvence mohou být konečný, jako v těchto příkladech, nebo nekonečný, jako je posloupnost všech dokonce kladná celá čísla (2, 4, 6, ...).
Pozice prvku v sekvenci je jeho hodnost nebo index; je to přirozené číslo, pro které je prvkem obrázek. První prvek má index 0 nebo 1, v závislosti na kontextu nebo konkrétní konvenci. v matematická analýza, je sekvence často označována písmeny ve formě , a , kde je dolní index n Odkazuje na nth prvek posloupnosti;[1] například ntého prvku Fibonacciho sekvence je obecně označován jako .
v výpočetní a počítačová věda, konečné sekvence se někdy nazývají struny, slova nebo seznamy, různá jména obvykle odpovídají různým způsobům jejich zastoupení paměť počítače; jsou volány nekonečné sekvence proudy. Prázdná posloupnost () je zahrnuta ve většině pojmů sekvence, ale může být vyloučena v závislosti na kontextu.

Příklady a notace
Sekvenci lze považovat za seznam prvků s určitým řádem.[2][3] Sekvence jsou užitečné pro studium mnoha matematických disciplín funkce, mezery a další matematické struktury využívající konvergence vlastnosti sekvencí. Základem jsou zejména sekvence série, které jsou důležité v diferenciální rovnice a analýza. Sekvence jsou také zajímavé samy o sobě a lze je studovat jako vzory nebo hlavolamy, například při studiu prvočísla.
Existuje řada způsobů, jak označit sekvenci, z nichž některé jsou užitečnější pro konkrétní typy sekvencí. Jedním ze způsobů, jak určit sekvenci, je vypsat všechny její prvky. Například první čtyři lichá čísla tvoří sekvenci (1, 3, 5, 7). Tato notace se používá také pro nekonečné sekvence. Například nekonečná posloupnost kladných lichých celých čísel je zapsána jako (1, 3, 5, 7, ...). Protože zaznamenávání sekvencí pomocí elipsa vede k nejednoznačnosti, výpis je nejužitečnější pro obvyklé nekonečné sekvence, které lze snadno rozpoznat z prvních několika prvků. Další způsoby označení sekvence jsou diskutovány po příkladech.
Příklady

The prvočísla jsou přirozená čísla větší než 1, které nemají č dělitele ale 1 a oni sami. Když je vezmeme v jejich přirozeném pořadí, získáme sekvenci (2, 3, 5, 7, 11, 13, 17, ...). Prvočísla jsou široce používána v matematika, zejména v teorie čísel kde existuje mnoho souvisejících výsledků.
The Fibonacciho čísla obsahují celočíselnou sekvenci, jejíž prvky jsou součtem předchozích dvou prvků. První dva prvky jsou buď 0 a 1 nebo 1 a 1, takže sekvence je (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...).[2]
Mezi další příklady sekvencí patří sekvence složené z racionální čísla, reálná čísla a komplexní čísla. Posloupnost (.9, 0,99, 0,999, 0,9999, ...) se například blíží číslu 1. Ve skutečnosti lze každé reálné číslo zapsat jako omezit posloupnosti racionálních čísel (např. prostřednictvím desítkové rozšíření ). Jako další příklad π je limit posloupnosti (3, 3.1, 3.14, 3.141, 3.1415, ...), který se zvyšuje. Související sekvence je sekvence desítkových číslic π, tj. (3, 1, 4, 1, 5, 9, ...). Na rozdíl od předchozí sekvence nemá tato sekvence žádný vzor, který je snadno rozeznatelný kontrolou.
Pro velký seznam příkladů celočíselných sekvencí viz On-line encyklopedie celočíselných sekvencí.
Indexování
Jiné notace mohou být užitečné pro sekvence, jejichž vzor nelze snadno uhodnout, nebo pro sekvence, které nemají vzor, jako jsou číslice π. Jedním z takových zápisů je napsat obecný vzorec pro výpočet nth termín jako funkce n, uzavřete jej do závorek a zahrňte dolní index označující sadu hodnot, které n můžu vzít. Například v této notaci by mohla být sekvence sudých čísel zapsána jako . Posloupnost čtverců lze zapsat jako . Proměnná n se nazývá index a sada hodnot, které může nabývat, se nazývá sada indexů.
Často je užitečné kombinovat tento zápis s technikou zpracování prvků sekvence jako jednotlivých proměnných. Tím se získají výrazy jako , což označuje sekvenci, jejíž ntento prvek je dán proměnnou . Například:
Jeden může zvážit více sekvencí současně pomocí různých proměnných; např. může být jiná sekvence než . Lze dokonce uvažovat o posloupnosti posloupností: označuje sekvenci, jejíž mth termín je sekvence .
Alternativou k zápisu domény sekvence do dolního indexu je označení rozsahu hodnot, které index může nabývat, a to uvedením jeho nejvyšší a nejnižší legální hodnoty. Například notace označuje desetidenní posloupnost čtverců . Limity a jsou povoleny, ale nepředstavují platné hodnoty pro index, pouze supremum nebo infimum těchto hodnot. Například sekvence je stejný jako sekvence , a neobsahuje další výraz „v nekonečnu“. Sekvence je b-nekonečná sekvence, a lze jej také zapsat jako .
V případech, kdy je pochopena sada indexovacích čísel, jsou dolní a horní indexy často vynechány. To znamená, že člověk jednoduše píše pro libovolnou sekvenci. Často index k rozumí se od 1 do run. Sekvence jsou však často indexovány počínaje od nuly, jako v
V některých případech jsou prvky sekvence přirozeně příbuzné sekvenci celých čísel, jejichž vzor lze snadno odvodit. V těchto případech může být sada indexů implikována seznamem prvních několika abstraktních prvků. Například posloupnost čtverců lichá čísla lze označit některým z následujících způsobů.
Kromě toho mohly být dolní a horní indexy ponechány ve třetí, čtvrté a páté notaci, pokud by byla indexovací sada chápána jako přirozená čísla. Ve druhé a třetí odrážce je přesně definovaná sekvence , ale není to stejné jako posloupnost označená výrazem.
Definování sekvence rekurzí
Sekvence, jejichž prvky přímo souvisejí s předchozími prvky, jsou často definovány pomocí rekurze. To je v rozporu s definicí posloupností prvků jako funkcí jejich pozic.
Chcete-li definovat sekvenci rekurzí, potřebujete pravidlo nazvané relace opakování postavit každý prvek z hlediska prvků před ním. Kromě toho musí být k dispozici dostatek počátečních prvků, aby bylo možné všechny následující prvky sekvence vypočítat postupnými aplikacemi relace opakování.
The Fibonacciho sekvence je jednoduchý klasický příklad, definovaný relací opakování
s počátečními podmínkami a . Z toho jednoduchý výpočet ukazuje, že prvních deset členů této posloupnosti je 0, 1, 1, 2, 3, 5, 8, 13, 21 a 34.
Složitý příklad posloupnosti definované relací opakování je Recamánova sekvence,[4] definované relací opakování
s počátečním termínem
A lineární opakování s konstantními koeficienty je relace opakování formuláře
kde jsou konstanty. Existuje obecná metoda pro vyjádření obecného pojmu takové posloupnosti jako funkce n; vidět Lineární opakování. V případě Fibonacciho sekvence jeden má a výsledná funkce n darováno Binetův vzorec.
A holonomická sekvence je sekvence definovaná relací opakování formuláře
kde jsou polynomy v n. Pro většinu holonomických sekvencí neexistuje žádný výslovný vzorec pro výslovné vyjádření jako funkce n. Holonomické sekvence přesto hrají důležitou roli v různých oblastech matematiky. Například mnoho speciální funkce mít Taylor série jehož posloupnost koeficientů je holonomická. Použití relace opakování umožňuje rychlý výpočet hodnot těchto speciálních funkcí.
Ne všechny sekvence lze určit relací opakování. Příkladem je posloupnost prvočísla v jejich přirozeném pořadí (2, 3, 5, 7, 11, 13, 17, ...).
Formální definice a základní vlastnosti
V matematice existuje mnoho různých pojmů posloupností, z nichž některé (např., přesná sekvence ) nejsou pokryty níže uvedenými definicemi a notacemi.
Definice
V tomto článku je sekvence formálně definována jako funkce jehož doména je interval z celá čísla. Tato definice zahrnuje několik různých použití slova „sekvence“, včetně jednostranných nekonečných sekvencí, bi-nekonečných sekvencí a konečných sekvencí (definice těchto druhů sekvencí viz níže). Mnoho autorů však používá užší definici tím, že požaduje, aby doménou sekvence byla množina přirozená čísla. Tato užší definice má tu nevýhodu, že vylučuje konečné posloupnosti a bi-nekonečné posloupnosti, které se ve standardní matematické praxi obvykle nazývají posloupnosti. Další nevýhodou je, že pokud někdo odstraní první členy posloupnosti, potřebuje znovu indexovat zbývající pojmy pro přizpůsobení této definici. V některých kontextech, aby se zkrátila expozice, codomain posloupnosti je stanoven kontextem, například požadavkem, aby to byla množina R reálných čísel,[5] sada C komplexních čísel,[6] nebo a topologický prostor.[7]
Ačkoli jsou sekvence typem funkce, obvykle se značně odlišují od funkcí v tom, že vstup je zapsán spíše jako dolní index než v závorkách, to znamená, An spíše než A(n). Existují také terminologické rozdíly: hodnota sekvence na nejnižším vstupu (často 1) se nazývá „první prvek“ sekvence, hodnota na druhém nejmenším vstupu (často 2) se nazývá „druhý prvek“, atd. Také, zatímco funkce abstrahovaná od jejího vstupu je obvykle označena jedním písmenem, např F, posloupnost abstrahovaná od jejího vstupu je obvykle psána notací jako např , nebo stejně Tady A je doména nebo sada indexů sekvence.
Sekvence a jejich limity (viz níže) jsou důležité koncepty pro studium topologických prostorů. Důležitým zobecněním sekvencí je koncept sítě. A síť je funkce z (případně nespočet ) řízená sada do topologického prostoru. Značkové konvence pro sekvence obvykle platí i pro sítě.
Konečný a nekonečný
The délka sekvence je definován jako počet termínů v sekvenci.
Posloupnost konečné délky n se také nazývá n-tuple. Mezi konečné posloupnosti patří prázdná sekvence (), který nemá žádné prvky.
Normálně termín nekonečná posloupnost odkazuje na posloupnost, která je nekonečná v jednom směru a konečná v druhém - posloupnost má první prvek, ale žádný finální prvek. Taková sekvence se nazývá a jednotlivě nekonečná posloupnost nebo a jednostranný nekonečný sled když je nutná disambiguation. Naproti tomu sekvence, která je nekonečná v obou směrech - tj. který nemá ani první, ani poslední prvek - nazývá se a b-nekonečná sekvence, obousměrná nekonečná sekvencenebo dvojnásobně nekonečná sekvence. Funkce ze sady Z z Všechno celá čísla do množiny, jako je například posloupnost všech sudých celých čísel (..., −4, −2, 0, 2, 4, 6, 8 ...), je bi-nekonečná. Tuto sekvenci lze označit .
Zvyšování a snižování
Sekvence se říká, že je monotónně roste, pokud je každý člen větší nebo roven jednomu před ním. Například sekvence monotónně roste právě tehdy An+1 An pro všechny n ∈ N. Pokud je každý po sobě jdoucí člen přísně větší než (>) předchozí člen, pak se nazývá posloupnost přísně monotónně rostoucí. Sekvence je monotónně klesá, pokud je každé po sobě jdoucí období menší nebo rovno předchozímu období, a přísně monotónně klesá, pokud je každý přísně menší než předchozí. Pokud posloupnost narůstá nebo klesá, nazývá se a monotónní sekvence. Toto je zvláštní případ obecnějšího pojmu a monotónní funkce.
Podmínky neklesající a nezvyšující se se často používají místo vzrůstající a klesající aby se předešlo možné záměně s přísně se zvyšuje a přísně klesá, resp.
Ohraničený
Pokud posloupnost reálných čísel (An) je takový, že všechny výrazy jsou menší než nějaké skutečné číslo M, pak se říká, že sekvence je ohraničený shora. Jinými slovy to znamená, že existuje M takové, že pro všechny n, An ≤ M. Jakýkoli takový M se nazývá horní hranice. Stejně tak, pokud, pro některé skutečné m, An ≥ m pro všechny n větší než někteří N, pak je sekvence ohraničený zdola a cokoli takového m se nazývá a dolní mez. Pokud je sekvence ohraničená shora a ohraničená zespodu, pak se o ní říká, že je ohraničený.
Následky
A subsekvence dané sekvence je sekvence vytvořená z dané sekvence odstraněním některých prvků bez narušení relativních poloh zbývajících prvků. Například posloupnost kladných celých čísel (2, 4, 6, ...) je posloupností kladných celých čísel (1, 2, 3, ...). Pozice některých prvků se změní, když jsou odstraněny další prvky. Relativní polohy jsou však zachovány.
Formálně posloupnost sekvence je libovolná posloupnost formuláře , kde je přísně rostoucí posloupnost kladných celých čísel.
Jiné typy sekvencí
Některé další typy sekvencí, které lze snadno definovat, zahrnují:
- An celočíselná sekvence je posloupnost, jejíž členy jsou celá čísla.
- A polynomiální sekvence je posloupnost, jejíž termíny jsou polynomy.
- Pozitivní celočíselná sekvence se někdy nazývá multiplikativní, pokud Anm = An Am pro všechny páry n, m takhle n a m jsou coprime.[8] V jiných případech se sekvence často nazývají multiplikativní, pokud An = na1 pro všechny n. Navíc, a multiplikativní Fibonacciho sekvence[9] uspokojuje rekurzní vztah An = An−1 An−2.
- A binární sekvence je posloupnost, jejíž členy mají jednu ze dvou diskrétních hodnot, např. základna 2 hodnoty (0,1,1,0, ...), řada hodů mincí (hlavy / ocasy) H, T, H, H, T, ..., odpovědi na sadu otázek typu True nebo False ( T, F, T, T, ...) atd.
Limity a konvergence

Důležitou vlastností sekvence je konvergence. Pokud posloupnost konverguje, konverguje k určité hodnotě známé jako omezit. Pokud posloupnost konverguje k nějakému limitu, pak je konvergentní. Sekvence, která nekonverguje, je odlišný.
Neformálně má sekvence limit, pokud se prvky sekvence přiblíží a přiblíží k nějaké hodnotě (nazývá se limit posloupnosti) a stanou se a zůstanou svévolně blízko k , což znamená, že vzhledem k reálné číslo větší než nula, všechny kromě konečného počtu prvků sekvence mají vzdálenost od méně než .
Například sekvence zobrazené vpravo konverguje k hodnotě 0. Na druhé straně sekvence (který začíná 1, 8, 27, ...) a (které začínají -1, 1, -1, 1,…) se liší.
Pokud posloupnost konverguje, pak je hodnota, ke které konverguje, jedinečná. Tato hodnota se nazývá omezit sekvence. Limit konvergentní sekvence je obvykle označen . Li je divergentní sekvence, pak výraz nemá smysl.
Formální definice konvergence
Posloupnost reálných čísel konverguje k skutečné číslo pokud pro všechny , existuje přirozené číslo takové, že pro všechny my máme[5]
Li je posloupnost komplexních čísel spíše než posloupnost reálných čísel, lze tento poslední vzorec stále použít k definování konvergence s tím, že označuje komplexní modul, tj. . Li je posloupnost bodů v a metrický prostor, pak lze vzorec použít k definování konvergence, pokud je výraz je nahrazen výrazem , který označuje vzdálenost mezi a .
Aplikace a důležité výsledky
Li a jsou konvergentní sekvence, pak existují následující limity a lze je vypočítat takto:[5][10]
- pro všechna reálná čísla
- , za předpokladu, že
- pro všechny a
Navíc:
- Li pro všechny větší než někteří , pak .[A]
- (Veta o zmáčknutí )
Li je sekvence taková, že pro všechny a ,
pak je konvergentní a . - Pokud je sekvence ohraničený a monotóní pak je konvergentní.
- Sekvence je konvergentní právě tehdy, když jsou konvergovány všechny její podsekvence.
Cauchyovy sekvence
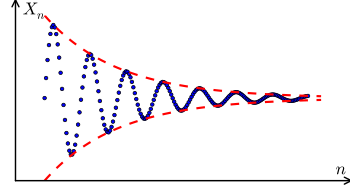
Cauchyova posloupnost je posloupnost, jejíž členy se libovolně přibližují k sobě, jak se n zvětší. Pojem Cauchyova sekvence je důležitý při studiu sekvencí v metrické prostory, a zejména v skutečná analýza. Jedním obzvláště důležitým výsledkem skutečné analýzy je Cauchyova charakterizace konvergence pro sekvence:
- Posloupnost reálných čísel je konvergentní (v reálných hodnotách) právě tehdy, je-li to Cauchy.
Naproti tomu existují Cauchyovy sekvence racionální čísla které nejsou v racionálních oblastech konvergentní, např. posloupnost definovanáX1 = 1 a Xn+1 = Xn + 2/Xn/2je Cauchy, ale nemá žádný racionální limit, srov. tady. Obecněji řečeno, každá posloupnost racionálních čísel, která konverguje k iracionální číslo je Cauchy, ale není konvergentní, když je interpretován jako posloupnost v sadě racionálních čísel.
Metrické prostory, které splňují Cauchyovu charakteristiku konvergence pro sekvence, se nazývají kompletní metrické prostory a jsou obzvláště pěkné pro analýzu.
Nekonečné limity
V kalkulu je běžné definovat notaci pro sekvence, které se nesbližují ve smyslu diskutovaném výše, ale které se místo toho stávají a zůstávají libovolně velké nebo se stávají a zůstávají libovolně negativní. Li se stane libovolně velkým jako , píšeme
V tomto případě říkáme, že sekvence rozchází senebo že to konverguje do nekonečna. Příkladem takové posloupnosti je An = n.
Li se stane libovolně záporným (tj. záporným a velkým) jako , píšeme
a řekněte, že sekvence rozchází se nebo konverguje do záporného nekonečna.
Série
A série je neformálně řečeno součet podmínek posloupnosti. To znamená, že se jedná o vyjádření formy nebo , kde je posloupnost reálných nebo komplexních čísel. The částečné částky řady jsou výrazy vyplývající z nahrazení symbolu nekonečna konečným číslem, tj Ndílčí součet série je číslo
Samotné částečné součty tvoří posloupnost , kterému se říká posloupnost dílčích součtů série . Pokud posloupnost dílčích součtů konverguje, pak říkáme, že řada je konvergentnía limit se nazývá hodnota série. Stejná notace se používá k označení řady a její hodnoty, tj. Píšeme .
Využití v jiných oblastech matematiky
Topologie
Sekvence hrají v topologii důležitou roli, zejména při studiu metrické prostory. Například:
- A metrický prostor je kompaktní přesně kdy to je postupně kompaktní.
- Funkce z metrického prostoru do jiného metrického prostoru je kontinuální přesně, když trvá konvergentní sekvence na konvergentní sekvence.
- Metrický prostor je a propojený prostor právě tehdy, kdykoli je prostor rozdělen na dvě sady, jedna ze dvou sad obsahuje sekvenci konvergující k bodu v druhé sadě.
- A topologický prostor je oddělitelný přesně, když existuje hustá posloupnost bodů.
Sekvence lze zobecnit na sítě nebo filtry. Tyto zobecnění umožňují jednomu rozšířit některé z výše uvedených vět na mezery bez metrik.
Topologie produktu
The topologický produkt posloupnosti topologických prostorů je kartézský součin těchto prostor vybavených a přírodní topologie volal topologie produktu.
Více formálně, vzhledem k posloupnosti mezer , produktový prostor
je definována jako množina všech sekvencí takové, že pro každého i, je prvek . The kanonické projekce jsou mapy pi : X → Xi definovaný rovnicí . Pak topologie produktu na X je definován jako nejhrubší topologie (tj. topologie s nejmenším počtem otevřených sad), pro které jsou všechny projekce pi jsou kontinuální. Topologie produktu se někdy nazývá Topologie Tychonoff.
Analýza
v analýza, když mluvíme o sekvencích, bude se obecně uvažovat o sekvencích formy
což znamená nekonečné sekvence prvků indexovaných pomocí přirozená čísla.
Může být vhodné mít sekvenci začínající indexem odlišným od 1 nebo 0. Například sekvenci definovanou pomocí Xn = 1/log (n) by bylo definováno pouze pro n ≥ 2. Když mluvíme o takových nekonečných posloupnostech, obvykle stačí (a pro většinu úvah se příliš nemění) předpokládat, že členové posloupnosti jsou definováni alespoň pro všechny indexy dostatečně velký, tj. větší než některé N.
Nejzákladnějším typem posloupnosti jsou číselné posloupnosti, tedy posloupnosti posloupnosti nemovitý nebo komplex čísla. Tento typ lze zobecnit na sekvence prvků některých vektorový prostor. Při analýze jsou uvažované vektorové prostory často funkční prostory. Ještě obecněji lze studovat sekvence s prvky v některých topologický prostor.
Sekvenční mezery
A sekvenční prostor je vektorový prostor jehož prvky jsou nekonečné posloupnosti nemovitý nebo komplex čísla. Ekvivalentně je to funkční prostor jehož prvky jsou funkce z přirozená čísla do pole K., kde K. je pole reálných čísel nebo pole komplexních čísel. Sada všech těchto funkcí je přirozeně identifikována se sadou všech možných nekonečných sekvencí s prvky v K., a lze jej změnit na vektorový prostor v rámci operací bodové sčítání funkcí a bodové skalární násobení. Všechny sekvenční prostory jsou lineární podprostory tohoto prostoru. Sekvenční prostory jsou obvykle vybaveny a norma, nebo alespoň struktura a topologický vektorový prostor.
Nejdůležitějšími sekvenčními prostory v analýze jsou ℓp prostory, skládající se z p-síla shrnutelných sekvencí s p-norma. Jedná se o speciální případy Lp mezery pro počítání opatření na množině přirozených čísel. Další důležité třídy sekvencí, jako jsou konvergentní sekvence nebo nulové sekvence formovat posloupnosti, respektive označené C a C0, s normou sup. Libovolný sekvenční prostor může být také vybaven topologie z bodová konvergence, pod kterým se stává zvláštním druhem Fréchetový prostor volal FK-prostor.
Lineární algebra
Sekvence nad a pole lze také zobrazit jako vektory v vektorový prostor. Konkrétně sada F-hodnocené sekvence (kde F je pole) je a funkční prostor (ve skutečnosti produktový prostor ) z F- ohodnocené funkce nad množinou přirozených čísel.
Abstraktní algebra
Abstraktní algebra využívá několik typů posloupností, včetně posloupností matematických objektů, jako jsou skupiny nebo prstence.
Zdarma monoid
Li A je sada, volný monoid přes A (označeno A*, také zvaný Kleene hvězda z A) je monoidní obsahující všechny konečné posloupnosti (nebo řetězce) nula nebo více prvků z A, s binární operací zřetězení. The bezplatná poloskupina A+ je podskupina z A* obsahující všechny prvky kromě prázdné sekvence.
Přesné sekvence
V kontextu teorie skupin posloupnost
z skupiny a skupinové homomorfismy je nazýván přesný, pokud obraz (nebo rozsah ) každého homomorfismu se rovná jádro z následujícího:
Pořadí skupin a homomorfismů může být buď konečné, nebo nekonečné.
Podobnou definici lze učinit pro některé další algebraické struktury. Například jeden může mít přesnou sekvenci vektorové prostory a lineární mapy nebo moduly a homomorfismy modulu.
Spektrální sekvence
v homologická algebra a algebraická topologie, a spektrální sekvence je prostředek pro výpočet skupin homologie pomocí postupných aproximací. Spektrální sekvence jsou zobecněním přesné sekvence, a od jejich zavedení do Jean Leray (1946 ), staly se důležitým výzkumným nástrojem, zejména v teorie homotopy.
Teorie množin
An pořadová indexovaná sekvence je zobecnění sekvence. Pokud α je a mezní pořadové číslo a X je množina, α-indexovaná sekvence prvků X je funkce od α do X. V této terminologii je ω indexovaná sekvence obyčejná sekvence.
Výpočetní
v počítačová věda se nazývají konečné posloupnosti seznamy. Jsou volány potenciálně nekonečné sekvence proudy. Jsou volány konečné posloupnosti znaků nebo číslic struny.
Proudy
Nekonečné sekvence číslice (nebo postavy ) čerpané z a konečný abeceda jsou zvláště zajímavé v teoretická informatika. Často se jim říká jednoduše sekvence nebo proudy, na rozdíl od konečných struny. Nekonečné binární sekvence jsou například nekonečné sekvence bity (znaky čerpané z abecedy {0, 1}). Sada C = {0, 1}∞ všech nekonečných binárních sekvencí se někdy nazývá Cantorův prostor.
Nekonečná binární sekvence může představovat a formální jazyk (sada řetězců) nastavením n th bit sekvence na 1 právě tehdy, když n th řetězec (v shortlexová objednávka ) je v jazyce. Toto znázornění je užitečné v metoda diagonalizace pro důkazy.[11]
Viz také
- Operace
- Příklady
- Signál diskrétního času
- Farey sekvence
- Fibonacciho sekvence
- Poslechněte si posloupnost
- Sekvence Thue – Morse
- Seznam celočíselných sekvencí
- Typy
- ± 1 sekvence
- Aritmetický postup
- Automatická sekvence
- Cauchyova posloupnost
- Konstantní rekurzivní sekvence
- Geometrický průběh
- Harmonický postup
- Holonomická sekvence
- Pravidelná sekvence
- Pseudonáhodná binární sekvence
- Náhodná sekvence
- Související pojmy
- Seznam (výpočet)
- Síť (topologie) (zobecnění sekvencí)
- Sekvence s pořadovým indexem
- Rekurze (informatika)
- Sada (matematika)
- Tuple
Poznámky
- ^ Všimněte si, že pokud jsou nerovnosti nahrazeny přísnými nerovnostmi, pak je to nepravda: Existují takové sekvence pro všechny , ale .
Reference
- ^ „Kompendium matematických symbolů“. Matematický trezor. 2020-03-01. Citováno 2020-08-17.
- ^ A b "Sekvence". www.mathsisfun.com. Citováno 2020-08-17.
- ^ Weisstein, Eric W. "Sekvence". mathworld.wolfram.com. Citováno 2020-08-17.
- ^ Sloane, N. J. A. (vyd.). „Sequence A005132 (Recamán's sequence)“. The On-line encyklopedie celočíselných sekvencí. Nadace OEIS. Citováno 26. ledna 2018.
- ^ A b C Gaughan, Edward (2009). „1.1 Sekvence a konvergence“. Úvod do analýzy. AMS (2009). ISBN 978-0-8218-4787-9.
- ^ Edward B. Saff a Arthur David Snider (2003). „Kapitola 2.1“. Základy komplexní analýzy. ISBN 978-01-390-7874-3.
- ^ James R. Munkres (2000). „Kapitoly 1 a 2“. Topologie. ISBN 978-01-318-1629-9.
- ^ Lando, Sergei K. (2003-10-21). "7.4 Multiplikativní sekvence". Přednášky o generování funkcí. AMS. ISBN 978-0-8218-3481-7.
- ^ Falcon, Sergio (2003). "Fibonacciho multiplikativní sekvence". International Journal of Mathematical Education in Science and Technology. 34 (2): 310–315. doi:10.1080/0020739031000158362. S2CID 121280842.
- ^ Dawikins, Paule. "Série a sekvence". Paul's Online Math Notes / Calc II (poznámky). Citováno 18. prosince 2012.
- ^ Oflazer, Kemal. „FORMÁLNÍ JAZYKY, AUTOMATA A VÝPOČET: ROZHODNUTÍ“ (PDF). cmu.edu. Carnegie-Mellon University. Citováno 24. dubna 2015.
externí odkazy
- "Sekvence", Encyclopedia of Mathematics, Stiskněte EMS, 2001 [1994]
- On-line encyklopedie celočíselných sekvencí
- Journal of Integer Sequences (volný, uvolnit)
- "Sekvence". PlanetMath.

































































































