Věty o izomorfismu - Isomorphism theorems

v matematika konkrétně abstraktní algebra, věty o izomorfismu (také známý jako Noetherovy věty o izomorfismu) jsou věty které popisují vztah mezi kvocienty, homomorfismy, a podobjekty. Verze teorémů existují pro skupiny, prsteny, vektorové prostory, moduly, Lež algebry a různé další algebraické struktury. v univerzální algebra, věty o izomorfismu lze zobecnit na kontext algeber a shody.

Dějiny

Věty o izomorfismu byly formulovány v nějaké obecnosti pro homomorfismy modulů pomocí Emmy Noetherová ve svém příspěvku Abstrakter Aufbau der Idealtheorie v algebraischen Zahl- und Funktionenkörpern, která byla vydána v roce 1927 v roce 2006 Mathematische Annalen. Méně obecné verze těchto vět lze nalézt v práci Richard Dedekind a předchozí příspěvky od Noether.

O tři roky později, B.L. van der Waerden zveřejnil svůj vlivný Algebra, první abstraktní algebra učebnice, která převzala skupiny -prsteny -pole přístup k předmětu. Van der Waerden připsal přednášky Noether dál teorie skupin a Emil Artin o algebře, stejně jako seminář vedený Artinem, Wilhelm Blaschke, Otto Schreier a sám van der Waerden ideály jako hlavní reference. Tři věty o izomorfismu zvané věta o homomorfismu, a dva zákony izomorfismu při použití na skupiny se zobrazí výslovně.

Skupiny

Nejprve představíme věty o izomorfismu z skupiny.

Poznámka k číslům a jménům

Níže uvádíme čtyři věty označené A, B, C a D. Často jsou očíslovány jako „první věta o izomorfismu“, „druhá ...“ atd .; neexistuje však univerzální dohoda o číslování. Zde uvádíme několik příkladů vět o izomorfismu skupiny (Všimněte si, že tyto věty mají analogie pro kroužky a moduly.) V literatuře:

Méně časté je zahrnutí věty D, obvykle známé jako „věta o mřížce „nebo„ věta o korespondenci “k jedné z vět o izomorfismu, ale pokud ano, je poslední.

Prohlášení o větách

Věta A

Schéma základní věty o homomorfismech

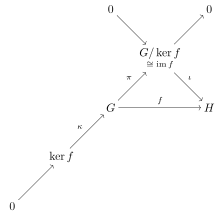
Nechat G a H být skupinami a nechat φ: G → H být homomorfismus. Pak:

1. The jádro z φ je normální podskupina z G,
2. The obraz z φ je podskupina z H, a
3. Obrázek uživatele φ je izomorfní do kvocientová skupina G / ker (φ).

Zejména pokud φ je surjektivní pak H je izomorfní s G / ker (φ).

Věta B

Schéma pro větu B

Nechat ${ displaystyle G}$ být skupina. Nechat ${ displaystyle S}$ být podskupinou ${ displaystyle G}$a nechte ${ displaystyle N}$ být normální podskupinou ${ displaystyle G}$. Pak platí následující:

1. The produkt ${ displaystyle SN}$ je podskupina ${ displaystyle G}$,
2. The průsečík ${ displaystyle S cap N}$ je normální podskupina ${ displaystyle S}$, a
3. Skupiny podílů ${ displaystyle (SN) / N}$ a ${ displaystyle S / (S cap N)}$ jsou izomorfní.

Technicky to není nutné ${ displaystyle N}$ být normální podskupinou, pokud ${ displaystyle S}$ je podskupinou normalizátor z ${ displaystyle N}$ v ${ displaystyle G}$. V tomto případě křižovatka ${ displaystyle S cap N}$ není normální podskupina ${ displaystyle G}$, ale stále je to normální podskupina ${ displaystyle S}$.

Tato věta se někdy nazývá „věta o izomorfismu“,^[8] "diamantová věta"^[10] nebo „teorém rovnoběžníku“.^[11]

Aplikace druhé věty o izomorfismu identifikuje projektivní lineární skupiny: například skupina na webu komplexní projektivní linie začíná nastavením ${ displaystyle G = GL_ {2} ( mathbb {C})}$, skupina invertibilních 2 × 2 komplexních matic, ${ displaystyle S = SL_ {2} ( mathbb {C})}$, podskupina matic determinantu 1 a ${ displaystyle N}$ normální podskupina skalárních matic ${ displaystyle mathbb {C} ^ { times} ! I = left {{ bigl (} { begin {smallmatrix} a & 0 0 & a end {smallmatrix}} { bigr)}: a v mathbb {C} ^ { times} vpravo }}$, my máme ${ displaystyle S cap N = { pm já }}$, kde ${ displaystyle I}$ je matice identity a ${ displaystyle SN = GL_ {2} ( mathbb {C})}$. Druhá teorém izomorfismu pak říká, že:

${ displaystyle PGL_ {2} ( mathbb {C}): = GL_ {2} ( mathbb {C}) / ( mathbb {C} ^ { times} ! I) cong SL_ {2} ( mathbb {C}) / { pm I } =: PSL_ {2} ( mathbb {C})}$

Věta C

Nechat ${ displaystyle G}$ být skupinou a ${ displaystyle N}$ normální podskupina ${ displaystyle G}$.Pak

1. Li ${ displaystyle K}$ je podskupina ${ displaystyle G}$ takhle ${ displaystyle N subseteq K subseteq G}$, pak ${ displaystyle G / N}$ má podskupinu isomorfní s ${ displaystyle K / N}$.
2. Každá podskupina ${ displaystyle G / N}$ je ve formě ${ displaystyle K / N}$ pro nějakou podskupinu ${ displaystyle K}$ z ${ displaystyle G}$ takhle ${ displaystyle N subseteq K subseteq G}$.
3. Li ${ displaystyle K}$ je normální podskupina ${ displaystyle G}$ takhle ${ displaystyle N subseteq K subseteq G}$, pak ${ displaystyle G / N}$ má normální podskupinu isomorfní s${ displaystyle K / N}$.
4. Každá normální podskupina ${ displaystyle G / N}$ je ve formě ${ displaystyle K / N}$, pro nějakou normální podskupinu ${ displaystyle K}$ z ${ displaystyle G}$ takhle ${ displaystyle N subseteq K subseteq G}$.
5. Li ${ displaystyle K}$ je normální podskupina ${ displaystyle G}$ takhle ${ displaystyle N subseteq K subseteq G}$, pak skupina podílů ${ displaystyle (G / N) / (K / N)}$ je izomorfní s ${ displaystyle G / K}$.

Věta D

The věta o korespondenci (také známý jako teorém o mřížce) se někdy nazývá věta o třetím nebo čtvrtém izomorfismu.

The Lemma Zassenhaus (také známý jako lemma motýla) se někdy nazývá čtvrtá věta o izomorfismu.^{[Citace je zapotřebí ]}

Diskuse

První věta o izomorfismu může být vyjádřena v kategorie teoretická jazyk tím, že kategorie skupin je (normální epi, mono) -faktorizovatelný; jinými slovy, normální epimorfismy a monomorfismy tvoří a faktorizační systém pro kategorii. To je zachyceno v komutativní diagram na okraji, který ukazuje objekty a morfismy, jejichž existenci lze odvodit z morfismu ${ displaystyle f: G rightarrow H}$. Diagram ukazuje, že každý morfismus v kategorii skupin má a jádro v kategorii teoretický význam; svévolný morfismus F faktory do ${ displaystyle iota circ pi}$, kde ι je monomorfismus a π je epimorfismus (v běžné kategorii jsou všechny epimorfismy normální). Toto je v diagramu reprezentováno objektem ${ displaystyle ker f}$ a monomorfismus ${ displaystyle kappa: ker f rightarrow G}$ (jádra jsou vždy monomorfismy), které doplňují zkratku přesná sekvence běží z levé dolní části do pravé horní části diagramu. Použití konvence přesné sekvence nám ušetří nutnost kreslit nulové morfismy z ${ displaystyle ker f}$ na ${ displaystyle H}$ a ${ displaystyle G / ker f}$.

Pokud je sekvence správně rozdělena (tj. Existuje morfismus σ že mapy ${ displaystyle G / ker f}$ do a π-předobraz sebe), pak G je polopřímý produkt normální podskupiny ${ displaystyle operatorname {im} kappa}$ a podskupina ${ displaystyle operatorname {im} sigma}$. Pokud je ponechána rozdělená (tj. Existuje, existuje ${ displaystyle rho: G rightarrow ker f}$ takhle ${ displaystyle rho circ kappa = operatorname {id} _ { ker f}}$), pak musí být také správně rozdělen, a ${ displaystyle operatorname {im} kappa times operatorname {im} sigma}$ je přímý produkt rozklad G. Obecně existence pravého rozdělení neznamená existenci levého rozdělení; ale v abelianská kategorie (například abelianské skupiny), levé rozdělení a pravé rozdělení jsou ekvivalentní s rozdělovací lemma, a pravé rozdělení stačí k vytvoření a přímý součet rozklad ${ displaystyle operatorname {im} kappa oplus operatorname {im} sigma}$. V kategorii abelianů jsou všechny monomorfismy také normální a diagram může být rozšířen o druhou krátkou přesnou sekvenci ${ displaystyle 0 rightarrow G / ker f rightarrow H rightarrow operatorname {coker} f rightarrow 0}$.

Ve druhé větě o izomorfismu je součin SN je připojit se z S a N v mřížka podskupin z G, zatímco křižovatka S ∩ N je setkat.

Třetí věta o izomorfismu je zobecněna pomocí devět lemma na abelianské kategorie a obecnější mapy mezi objekty.

Prsteny

Výroky vět pro prsteny jsou podobné, přičemž pojem normální podskupiny je nahrazen pojmem ideál.

Věta A

Nechat R a S být prsteny a nechat φ: R → S být kruhový homomorfismus. Pak:

1. The jádro z φ je ideál R,
2. The obraz z φ je podřízený z S, a
3. Obrázek uživatele φ je isomorfní s kvocientový kroužek R / ker (φ).

Zejména pokud φ je surjektivní pak S je izomorfní s R / ker (φ).

Věta B

Nechat R ložisko. Nechat S být podřetězcem Ra nechte Já být ideálem R. Pak:

1. Součet S + Já = {s + i | s ∈ S, i ∈ Já} je podřetězec R,
2. Křižovatka S ∩ Já je ideál S, a
3. Kvocient zazvoní (S + Já) / Já a S / (S ∩ Já) jsou izomorfní.

Věta C

Nechat R být prsten, a Já ideál R.Pak

1. Li ${ displaystyle A}$ je podřetězec z ${ displaystyle R}$ takhle ${ displaystyle I subseteq A subseteq R}$, pak ${ displaystyle A / I}$ je podřetězec z ${ displaystyle R / I}$.
2. Každý podřízený řetězec ${ displaystyle R / I}$ je ve formě ${ displaystyle A / I}$, pro některé podřetězce ${ displaystyle A}$ z ${ displaystyle R}$ takhle ${ displaystyle I subseteq A subseteq R}$.
3. Li ${ displaystyle J}$ je ideál ${ displaystyle R}$ takhle ${ displaystyle I subseteq J subseteq R}$, pak ${ displaystyle J / I}$ je ideál ${ displaystyle R / I}$.
4. Každý ideál ${ displaystyle R / I}$ je ve formě ${ displaystyle J / I}$, pro nějaký ideální ${ displaystyle J}$ z ${ displaystyle R}$ takhle ${ displaystyle I subseteq J subseteq R}$.
5. Li ${ displaystyle J}$ je ideál ${ displaystyle R}$ takhle ${ displaystyle I subseteq J subseteq R}$, pak kvocientový kroužek ${ displaystyle (R / I) / (J / I)}$ je izomorfní s ${ displaystyle R / J}$.

Věta D

Nechat ${ displaystyle I}$ být ideálem ${ displaystyle R}$. Korespondence ${ displaystyle A leftrightarrow A / I}$ je zahrnutí zachovávající bijekci mezi sadou podřetězců ${ displaystyle A}$ z ${ displaystyle R}$ které obsahují ${ displaystyle I}$ a soubor podřetězců ${ displaystyle R / I}$. Dále ${ displaystyle A}$ (podřetězec obsahující ${ displaystyle I}$) je ideál ${ displaystyle R}$ kdyby a jen kdyby ${ displaystyle A / I}$ je ideál ${ displaystyle R / I}$.^[12]

Moduly

Výroky vět o izomorfismu pro moduly jsou obzvláště jednoduché, protože je možné vytvořit a kvocientový modul od kteréhokoli submodul. Věty o izomorfismu pro vektorové prostory (moduly nad polem) a abelianské skupiny (moduly přes ${ displaystyle mathbb {Z}}$) jsou jejich speciální případy. U konečných trojrozměrných vektorových prostorů všechny tyto věty vyplývají z věta o nulitě.

V následujícím textu bude „modul“ znamenat „R-module "pro nějaký pevný kruh R.

Věta A

Nechat M a N být moduly a nechat φ: M → N být homomorfismus modulu. Pak:

1. The jádro z φ je submodul M,
2. The obraz z φ je submodul N, a
3. Obrázek uživatele φ je isomorfní s kvocientový modul M / ker (φ).

Zejména pokud φ je tedy surjektivní N je izomorfní s M / ker (φ).

Věta B

Nechat M být modulem a nechat S a T být podmoduly M. Pak:

1. Součet S + T = {s + t | s ∈ S, t ∈ T} je submodul M,
2. Křižovatka S ∩ T je submodul M, a
3. Kvocientové moduly (S + T) / T a S / (S ∩ T) jsou izomorfní.

Věta C

Nechat M být modulem, T submodul M.

1. Li ${ displaystyle S}$ je submodul ${ displaystyle M}$ takhle ${ displaystyle T subseteq S subseteq M}$, pak ${ displaystyle S / T}$ je submodul ${ displaystyle M / T}$.
2. Každý submodul ${ displaystyle M / T}$ je ve formě ${ displaystyle S / T}$, pro nějaký submodul ${ displaystyle S}$ z ${ displaystyle M}$ takhle ${ displaystyle T subseteq S subseteq M}$.
3. Li ${ displaystyle S}$ je submodul ${ displaystyle M}$ takhle ${ displaystyle T subseteq S subseteq M}$, pak modul kvocientu ${ displaystyle (M / T) / (S / T)}$ je izomorfní s ${ displaystyle M / S}$.

Věta D

Nechat ${ displaystyle M}$ být modulem, ${ displaystyle N}$ submodul ${ displaystyle M}$. Mezi dílčími moduly z ${ displaystyle M}$ které obsahují ${ displaystyle N}$ a podmoduly ${ displaystyle M / N}$. Korespondence je dána ${ displaystyle A leftrightarrow A / N}$ pro všechny ${ displaystyle A supseteq N}$. Tato korespondence dojíždí s procesy přijímání součtů a křižovatek (tj. Je mřížkový izomorfismus mezi mřížkou podmodulů ${ displaystyle M / N}$ a mřížka submodulů ${ displaystyle M}$ které obsahují ${ displaystyle N}$).^[13]

Všeobecné

Zobecnit to na univerzální algebra, normální podskupiny musí být nahrazeny kongruenční vztahy.

A shoda na algebra ${ displaystyle A}$ je vztah ekvivalence ${ displaystyle Phi subseteq A krát A}$ která tvoří subalgebru ${ displaystyle A krát A}$ považována za algebru s komponentními operacemi. Lze vytvořit sadu tříd ekvivalence ${ displaystyle A / Phi}$ do algebry stejného typu definováním operací prostřednictvím zástupců; od té doby to bude dobře definované ${ displaystyle Phi}$ je subalgebra ${ displaystyle A krát A}$. Výsledná struktura je kvocient algebra.

Věta A

Nechat ${ displaystyle f: A rightarrow B}$ být algebra homomorfismus. Pak obrázek ${ displaystyle f}$ je subalgebra ${ displaystyle B}$, vztah daný ${ displaystyle Phi: f (x) = f (y)}$ (tj jádro z ${ displaystyle f}$) je kongruence na ${ displaystyle A}$a algebry ${ displaystyle A / Phi }$ a ${ displaystyle operatorname {im} f}$ jsou izomorfní. (Pamatujte, že v případě skupiny ${ displaystyle f (x) = f (y)}$ iff ${ displaystyle f (xy ^ {- 1}) = 1}$, takže člověk získá představu o jádře použitém v teorii grup v tomto případě.)

Věta B

Vzhledem k algebře ${ displaystyle A}$, subalgebra ${ displaystyle B}$ z ${ displaystyle A}$a shoda ${ displaystyle Phi}$ na ${ displaystyle A}$, nechť ${ displaystyle Phi _ {B} = Phi cap (B krát B)}$ být stopou ${ displaystyle Phi}$ v ${ displaystyle B}$ a ${ displaystyle [B] ^ { Phi} = {K v A / Phi: K cap B neq emptyset }}$ kolekce tříd ekvivalence, které se protínají ${ displaystyle B}$. Pak

1. ${ displaystyle Phi _ {B}}$ je shoda na ${ displaystyle B}$,
2. ${ displaystyle [B] ^ { Phi}}$ je subalgebra ${ displaystyle A / Phi}$, a
3. algebra ${ displaystyle [B] ^ { Phi}}$ je izomorfní s algebrou ${ displaystyle B / Phi _ {B}}$.

Věta C

Nechat ${ displaystyle A}$ být algebra a ${ displaystyle Phi, Psi}$ dva shodné vztahy na ${ displaystyle A}$ takhle ${ displaystyle Psi subseteq Phi}$. Pak ${ displaystyle Phi / Psi = {([a '] _ { Psi}, [a' '] _ { Psi}) :( a', a '') in Phi } = [ ] _ { Psi} circ Phi circ [] _ { Psi} ^ {- 1}}$ je shoda na ${ displaystyle A / Psi}$, a ${ displaystyle A / Phi}$ je izomorfní s ${ displaystyle (A / Psi) / ( Phi / Psi)}$.

Věta D

Nechat ${ displaystyle A}$ být algebra a označovat ${ displaystyle operatorname {Con} A}$ soubor všech kongruencí na ${ displaystyle A}$. Sada${ displaystyle operatorname {Con} A}$ je úplná mříž nařízená začleněním.^[14]Li ${ displaystyle Phi in operatorname {Con} A}$ je shoda a označujeme tím ${ displaystyle left [ Phi, A krát A right] subseteq operatorname {Con} A}$ soubor všech shod, které obsahují ${ displaystyle Phi}$ (tj. ${ displaystyle left [ Phi, A krát A right]}$ je jistina filtr v ${ displaystyle operatorname {Con} A}$, navíc je to sublattice), poté mapa ${ displaystyle alpha: left [ Phi, A krát A right] to operatorname {Con} (A / Phi), Psi mapsto Psi / Phi}$ je mřížkový izomorfismus.^[15][16]

Poznámka

Reference

• Emmy Noetherová, Abstrakter Aufbau der Idealtheorie v algebraischen Zahl- und Funktionenkörpern, Mathematische Annalen 96 (1927), str. 26–61
• Colin McLarty „Topologie Emmy Noetherové„ Set Theoretic “: Od Dedekinda po vzestup funktorů“. Architektura moderní matematiky: Pokusy o historii a filozofii (editoval Jeremy Gray a José Ferreirós), Oxford University Press (2006), s. 211–35.
• Jacobson, Nathan (2009), Základní algebra, 1 (2. vyd.), Dover, ISBN  9780486471891
• Paul M. Cohn, Univerzální algebra, Kapitola II.3 s. 57
• Milne, James S. (2013), Skupinová teorie, 3.13
• van der Waerden, B. I. (1994), Algebra, 1 (9. vyd.), Springer-Verlag
• Dummit, David S .; Foote, Richard M. (2004). Abstraktní algebra. Hoboken, NJ: Wiley. ISBN  978-0-471-43334-7.
• Burris, Stanley; Sankappanavar, H. P. (2012). Kurz univerzální algebry (PDF). ISBN  978-0-9880552-0-9.
• W. R. Scott (1964), Skupinová teorie, Prentice Hall
• John R. Durbin (2009). Moderní algebra: Úvod (6. vyd.). Wiley. ISBN  978-0-470-38443-5.
• Anthony W. Knapp (2016), Základní algebra (Digitální druhé vydání)
• Pierre Antoine Grillet (2007), Abstraktní algebra (2. vyd.), Springer
• Joseph J. Rotman (2003), Pokročilá moderní algebra (2. vyd.), Prentice Hall, ISBN  0130878685