Injekční funkce - Injective function
| Funkce | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X ↦ F (X) | |||||||||||||||||||||||||||||||||
| Příklady od doména a codomain | |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| Třídy / vlastnosti | |||||||||||||||||||||||||||||||||
| Konstantní · Identita · Lineární · Polynomiální · Racionální · Algebraický · Analytický · Hladký · Kontinuální · Měřitelný · Injekční · Surjective · Bijective | |||||||||||||||||||||||||||||||||
| Stavby | |||||||||||||||||||||||||||||||||
| Omezení · Složení · λ · Inverzní | |||||||||||||||||||||||||||||||||
| Zobecnění | |||||||||||||||||||||||||||||||||
| Částečný · Více hodnot · Implicitní | |||||||||||||||||||||||||||||||||
v matematika, an injekční funkce (také známý jako injekcenebo funkce jedna ku jedné) je funkce že mapy odlišný jeho prvky doména k jeho odlišným prvkům codomain.[1] Jinými slovy, každý prvek codomainu funkce je obraz z nejvíce jeden prvek její domény.[2] Termín funkce jedna ku jedné nesmí být zaměňována s osobní korespondence který odkazuje na bijektivní funkce, což jsou funkce takové, že každý prvek v doméně je obrazem přesně jednoho prvku v doméně.

Injekční non-surjektivní funkce (injekce, ne a bijekce )
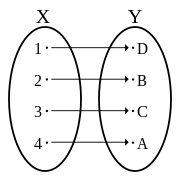
Injekční surjektivní funkce (bijekce )
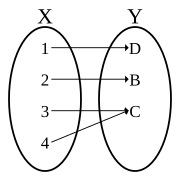
Neinjekční surjektivní funkce (surjection, ne a bijekce )
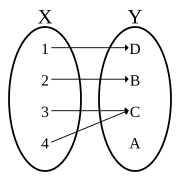
Neinjekční nesurjektivní funkce (také ne a bijekce )
A homomorfismus mezi algebraické struktury je funkce, která je kompatibilní s operacemi struktur. Pro všechny běžné algebraické struktury a zejména pro vektorové prostory, an injekční homomorfismus se také nazývá a monomorfismus. V obecnějším kontextu teorie kategorií, definice monomorfismu se liší od definice injekčního homomorfismu.[3] Toto je tedy věta, že jsou ekvivalentní pro algebraické struktury; vidět Homomorfismus § Monomorfismus Více podrobností.
Funkce F to není injective se někdy nazývá mnoho k jednomu.[2]
Definice
Nechat F být funkce jehož doména je sada X. Funkce F se říká, že je injekční za předpokladu, že pro všechny A a b v Xkdykoli F(A) = F(b), pak A = b; to je F(A) = F(b) naznačuje A = b. Ekvivalentně, pokud A ≠ b, pak F(A) ≠ F(b).
Symbolicky,
což je logicky ekvivalentní s kontrapozitivní,
Příklady
- Pro jakoukoli sadu X a jakákoli podmnožina S z X, mapa zařazení S → X (který odesílá libovolný prvek s z S pro sebe) je injekční. Zejména funkce identity X → X je vždy injektivní (a ve skutečnosti bijektivní).
- Pokud doména X = ∅ nebo X má pouze jeden prvek, pak funkci X → Y je vždy injekční.
- Funkce F : R → R definován F(X) = 2X + 1 je injekční.
- Funkce G : R → R definován G(X) = X2 je ne injekční, protože (například) G(1) = 1 = G(−1). Pokud však G je předefinováno tak, že jeho doménou jsou tedy nezáporná reálná čísla [0, + ∞] G je injekční.
- The exponenciální funkce exp: R → R definován exp (X) = EX je injekční (ale ne surjektivní, protože žádná skutečná hodnota není mapována na záporné číslo).
- The přirozený logaritmus funkce ln: (0, ∞) → R definován X N ln X je injekční.
- Funkce G : R → R definován G(X) = Xn − X není injekční, protože například G(0) = G(1) = 0.
Obecněji, kdy X a Y jsou oba skutečná linie R, potom injekční funkce F : R → R je graf, jehož graf nikdy neprotíná žádnou vodorovnou čarou více než jednou. Tento princip se označuje jako test vodorovné čáry.[2]
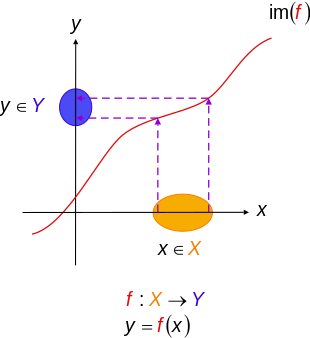
Injekce lze vrátit zpět
Funkce s levé inverze jsou vždy injekce. To je dané F : X → Y, pokud existuje funkce G : Y → X tak, že pro každého X ∈ X,
- G(F(X)) = X (F lze vrátit zpět G), pak F je injekční. V tomto případě, G se nazývá a odvolání z F. Naopak, F se nazývá a sekce z G.
Naopak každá injekce F s neprázdnou doménou má levou inverzní funkci G, které lze definovat upevněním prvku A v doméně F aby G(X) se rovná jedinečnému obrazu X pod F pokud existuje a G(X) = A v opačném případě.[6]
Levá inverze G není nutně inverzní z F, protože složení v opačném pořadí, F ∘ G, se mohou lišit od identity na Y. Jinými slovy, injektivní funkce může být „obrácena“ levou inverzí, ale není to nezbytně nutné invertibilní, což vyžaduje, aby funkce byla bijektivní.
Injekce mohou být invertovatelné
Ve skutečnosti otočit injekční funkci F : X → Y do bijektivní (proto invertibilní ), stačí nahradit jeho codomain Y podle skutečného rozsahu J = F(X). To je, pojďme G : X → J takhle G(X) = F(X) pro všechny X v X; pak G je bijektivní. Vskutku, F lze započítat jako včJ,Y ∘ G, kde včJ,Y je funkce začlenění z J do Y.
Obecněji řečeno, injekční dílčí funkce se nazývají částečné bijekce.
Další vlastnosti
- Li F a G jsou tedy injekční F ∘ G je injekční.

- Li G ∘ F je tedy injekční F je injekční (ale G nemusí být).
- F : X → Y je injektivní tehdy a jen tehdy, pokud jsou dané nějaké funkce G, h : Ž → X kdykoli F ∘ G = F ∘ h, pak G = h. Jinými slovy, injektivní funkce jsou přesně ty monomorfismy v kategorie Soubor sad.
- Li F : X → Y je injekční a A je podmnožina z X, pak F −1(F(A)) = A. Tím pádem, A lze získat z jeho obraz F(A).
- Li F : X → Y je injekční a A a B jsou obě podmnožiny X, pak F(A ∩ B) = F(A) ∩ F(B).
- Každá funkce h : Ž → Y lze rozložit jako h = F ∘ G pro vhodnou injekci F a surjection G. Tento rozklad je jedinečný až do izomorfismu, a F lze považovat za funkce začlenění rozsahu h(Ž) z h jako podmnožina codomain Y z h.
- Li F : X → Y je tedy injekční funkce Y má alespoň tolik prvků jako X, ve smyslu základní čísla. Zejména pokud navíc existuje injekce z Y na X, pak X a Y mít stejné hlavní číslo. (Toto je známé jako Cantor – Bernstein – Schroederova věta.)
- Pokud obojí X a Y jsou konečný se stejným počtem prvků F : X → Y je injektivní tehdy a jen tehdy F je surjektivní (v jakém případě F je bijektivní ).
- Injekční funkce, která je a homomorfismus mezi dvěma algebraickými strukturami je vkládání.
- Na rozdíl od surjektivity, což je vztah mezi grafem funkce a její doménou, je injektivita vlastnost grafu samotné funkce; to znamená, zda funkce F je injective lze rozhodnout pouze s ohledem na graf (a nikoli codomain) z F.
Dokazující, že funkce jsou injektivní
Důkaz, že funkce F Je injektivní závisí na tom, jak je funkce prezentována a jaké vlastnosti má funkce. U funkcí, které jsou dány nějakým vzorcem, existuje základní myšlenka. Používáme definici injektivity, konkrétně že pokud F(X) = F(y), pak X = y.[7]
Zde je příklad:
- F = 2X + 3
Důkaz: Let F : X → Y. Předpokládat F(X) = F(y). Tak 2X + 3 = 2y + 3 ⇒ 2X = 2y ⇒ X = y. Z definice tedy vyplývá, že F je injekční.
Existuje několik dalších metod prokazování, že je funkce injektivní. Například v počtu, pokud F je diferencovatelná funkce definovaná v nějakém intervalu, pak stačí ukázat, že derivace je v daném intervalu vždy kladná nebo vždy záporná. V lineární algebře, pokud F je lineární transformace, stačí ukázat, že jádro F obsahuje pouze nulový vektor. Li F je funkce s konečnou doménou, stačí prohledat seznam obrázků každého prvku domény a zkontrolovat, zda se v seznamu dvakrát neobjeví žádný obrázek.
Grafický přístup k funkci se skutečnou hodnotou F skutečné proměnné X je test vodorovné čáry. Pokud každá vodorovná čára protíná křivku f (x) tedy maximálně v jednom bodě F je injekční nebo jedna ku jedné.
Viz také
Poznámky
- ^ „Definitivní glosář vyššího matematického žargonu - jedna k jedné“. Matematický trezor. 2019-08-01. Citováno 2019-12-07.
- ^ A b C „Injective, Surjective and Bijective“. www.mathsisfun.com. Citováno 2019-12-07.
- ^ „Oddíl 7.3 (00V5): Injektivní a surjektivní mapy předvoleb - projekt Stacks“. stacks.math.columbia.edu. Citováno 2019-12-07.
- ^ „Bijection, Injection, And Surjection | Brilliant Math & Science Wiki“. brilliant.org. Citováno 2019-12-07.
- ^ Farlow, S. J. „Injekce, Surjekce a Bijekce“ (PDF). math.umaine.edu. Citováno 2019-12-06.
- ^ Na rozdíl od odpovídajícího tvrzení, že každá surjektivní funkce má inverzní právo, toto nevyžaduje axiom volby jako existence A je implikována prázdnotou domény. Toto tvrzení však může selhat v méně konvenční matematice, jako je konstruktivní matematika. V konstruktivní matematice inkluze {0,1} → R dvou prvků v reálných oblastech nemůže mít levou inverzní funkci, protože by to porušilo nerozložitelnost tím, že odvolání reálného řádku do množiny {0,1}.
- ^ Williams, Peter. „Proving Functions one-to-one“. Archivovány od originál dne 4. června 2017.
Reference
- Bartle, Robert G. (1976), Prvky reálné analýzy (2. vyd.), New York: John Wiley & Sons, ISBN 978-0-471-05464-1, str. 17 ff.
- Halmos, Paul R. (1974), Naivní teorie množin, New York: Springer, ISBN 978-0-387-90092-6, str. 38 ff.






