Plochý modul - Flat module - Wikipedia

v homologická algebra a algebraická geometrie, a plochý modul přes prsten R je R-modul M takové, že při tenzorový produkt přes R s M konzervuje přesné sekvence. Modul je věrně plochý pokud přijetí tenzorového produktu se sekvencí vytvoří přesnou sekvenci právě tehdy, pokud je původní sekvence přesná.

Plochost zavedl Serre  (1956 ) ve svém příspěvku Géometrie Algébrique et Géométrie Analytique. Viz také plochý morfismus.

Definice

Modul M přes prsten R je nazýván byt pokud je splněna následující podmínka: pro jakoukoli mapu vstřelení ${ displaystyle phi: K do L}$ z R-moduly, mapa

${ displaystyle K otimes _ {R} M až L otimes _ {R} M}$

vyvolané ${ Displaystyle k otimes m mapsto phi (k) otimes m}$ je injekční.

Jinými slovy, pro R- moduly K., L, a J, pokud ${ displaystyle 0 rightarrow K rightarrow L rightarrow J rightarrow 0}$ je tedy krátká přesná sekvence M je plochý modul přes R kdyby a jen kdyby ${ displaystyle 0 rightarrow K otimes _ {R} M rightarrow L otimes _ {R} M rightarrow J otimes _ {R} M rightarrow 0}$ je také krátká přesná sekvence.

Tato definice platí, i když R není nutně komutativní a M je levice R-modul a K. a L že jo R- moduly. Jediný rozdíl je v tomto případě ${ displaystyle K otimes _ {R} M}$ a ${ displaystyle L otimes _ {R} M}$ nejsou obecně R-moduly, ale pouze abelianské skupiny.

Charakterizace rovinnosti

Od tenzorování s M je pro jakýkoli modul M, pravý přesný funktor

${ displaystyle { textbf {Mod}} _ {R} do { textbf {Ab}}}$

(mezi kategorií R-moduly a abelianské skupiny), M je ploché právě tehdy, pokud je předchozí funktor přesný.

To může být také zobrazeno v podmínce definující rovinnost, jak je uvedeno výše, stačí vzít ${ displaystyle L = R}$, samotný prsten a ${ displaystyle K}$ konečně vygenerovaný ideál z R.

Rovinnost je také ekvivalentní následující rovnici, kterou lze parafrázovat tím, že to řekneme R-lineární vztahy, které platí M pramení z lineárních vztahů, které drží v R: pro každou lineární závislost, ${ displaystyle r ^ {T} x = součet _ {i = 1} ^ {k} r_ {i} x_ {i} = 0}$ s ${ displaystyle r_ {i} v R}$ a ${ displaystyle x_ {i} v M}$, existuje matice ${ displaystyle A v R ^ {k krát j}}$ a prvek ${ displaystyle y v M ^ {j}}$ takhle ${ displaystyle Ay = x}$ a ${ displaystyle r ^ {T} A = 0.}$^[1] Dále M je plochý právě tehdy, pokud platí následující podmínka: pro každou mapu ${ displaystyle f: F až M,}$ kde ${ displaystyle F}$ je konečně generovaný zdarma ${ displaystyle R}$-module a pro každý konečně vygenerovaný ${ displaystyle R}$-podmodul ${ displaystyle K}$ z ${ displaystyle ker f,}$ mapa ${ displaystyle f}$ faktory prostřednictvím mapy G zdarma ${ displaystyle R}$-modul ${ displaystyle G}$ takhle ${ displaystyle g (K) = 0:}$

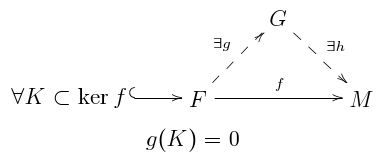
Příklady a vztahy k jiným pojmům

Rovinnost souvisí s různými dalšími podmínkami na modulu, například s volností, projektivitou nebo bez kroucení. To je částečně shrnuto v následující grafice:

Zdarma nebo projektivní moduly vs. ploché moduly

Zdarma moduly jsou ploché přes jakýkoli prsten R. To platí od funktoru

${ displaystyle L mapsto L otimes _ {R} ( bigoplus _ {i in I} R) cong bigoplus _ {i in I} L}$

je přesný. Například, vektorové prostory přes pole jsou ploché moduly. Přímé součty plochých modulů jsou opět ploché. Zejména, projektivní moduly (přímé součty volných modulů) jsou ploché. Naopak pro komutativní Noetherian ring R, definitivně generováno ploché moduly jsou projektivní.

Ploché vs. torzní moduly

Jakýkoli plochý modul je bez kroucení. Konverzace platí nad celými čísly a obecněji nad hlavní ideální domény. To vyplývá z výše uvedené charakterizace plochosti z hlediska ideálů. Obecněji řečeno, tato konverzace se drží Dedekind zazvoní.

Integrální doména se nazývá a Prüferova doména pokud je každý modul bez zkroucení nad ním plochý.

Plochost dokončení

Nechat ${ displaystyle A}$ být noetherianským prstenem a ${ displaystyle I}$ ideál. Pak dokončení ${ displaystyle A až { widehat {A}}}$ s ohledem na ${ displaystyle I}$ je plochá.^[2] Je věrně plochý právě tehdy ${ displaystyle I}$ je obsažen v Jacobsonově radikálu z ${ displaystyle A}$.^[3] (srov. Zariski prsten.)

Non-příklady

Kvocienty plochých modulů nejsou obecně ploché. Například pro každé celé číslo ${ displaystyle n> 1, mathbb {Z} / n mathbb {Z}}$ není úplně ${ displaystyle mathbb {Z},}$ protože ${ displaystyle n: mathbb {Z} až mathbb {Z}, x mapsto nx}$ je injekční, ale tenzorizovaný ${ displaystyle mathbb {Z} / n mathbb {Z}}$ Není. Podobně, ${ displaystyle mathbb {Q} / mathbb {Z}}$ není úplně ${ displaystyle mathbb {Z}.}$

Další vlastnosti trvalosti

Obecně libovolné přímé částky a filtrované kolimity (také známý jako přímé limity ) plochých modulů jsou ploché, což je důsledek skutečnosti, že tenzorový produkt dojíždí s přímými součty a filtrovanými kolimity (ve skutečnosti se všemi kolimity ), a že jak přímé součty, tak filtrované kolimity jsou přesné funktory. Zejména to ukazuje, že všechny filtrované kolimity volných modulů jsou ploché.

Lazard (1969) dokázal, že platí i konverzace: M je plochá, jen když je a přímý limit z konečně vygenerovaný bezplatné moduly. V důsledku toho lze odvodit, že každý konečně představen plochý modul je projektivní. přímý součet ${ displaystyle bigoplus nolimits _ {i v I} M_ {i}}$ je plochý právě tehdy, když každý ${ displaystyle M_ {i}}$ je plochá.

produkty bytu R- moduly nemusí být obecně ploché. Ve skutečnosti, Chase (1960) ukázal prsten R je koherentní (tj. jakýkoli konečně vygenerovaný ideál je konečně představen) právě tehdy, když jsou libovolné součiny bytu R-moduly jsou opět ploché.^[4]

Prodloužení plochého kroužku

Li ${ displaystyle phi: R až S}$ je prstenový homomorfismus, S se nazývá flat over R (nebo byt R-algebra), pokud je plochá jako R-modul. Například polynomiální kruh R[t] je úplně R, pro jakýkoli prsten R. Navíc pro všechny multiplikativně uzavřená podmnožina ${ displaystyle S}$ komutativního kruhu ${ displaystyle R}$, lokalizační kroužek ${ displaystyle S ^ {- 1} R}$ je naplocho R. Například, ${ displaystyle mathbb {Q}}$ je naplocho ${ displaystyle mathbb {Z}}$ (i když ne projektivní).

Nechat ${ displaystyle S = R [x_ {1}, tečky, x_ {r}]}$ být polynomiálním prstencem nad noetherianským kruhem ${ displaystyle R}$ a ${ displaystyle f v S}$ nonzerodivisor. Pak ${ displaystyle S / fS}$ je naplocho ${ displaystyle R}$ kdyby a jen kdyby ${ displaystyle f}$ je primitivní (koeficienty generují ideální jednotku).^[5] Tím se získá příklad plochého modulu, který není volný.

Kunz (1969) ukázal, že netherianský místní prsten ${ displaystyle R}$ pozitivní charakteristický p je pravidelný jen a jen pokud Frobeniův morfismus ${ displaystyle R až R, r mapsto r ^ {p}}$ je plochá a ${ displaystyle R}$ je snížena.

Prodloužení plochého kruhu jsou důležitá v algebře, algebraické geometrii a souvisejících oblastech. Morfismus ${ displaystyle f: X až Y}$ z schémata je plochý morfismus pokud podle jedné z několika ekvivalentních definic indukovaná mapa na místních prstencích

${ displaystyle { mathcal {O}} _ {Y, f (x)} až { mathcal {O}} _ {X, x}}$

je homomorfismus plochého kruhu pro jakýkoli bod X v X. Výše uvedené vlastnosti plochých (nebo věrně plochých) morfismů stanovených metodami komutativní algebry se tedy překládají do geometrických vlastností plochých morfismů v algebraické geometrii.

Místní aspekty rovinnosti nad komutativními kruhy

V této části prsten R má být komutativní. V této situaci je plochost R-modules souvisí několika způsoby s pojmem lokalizace: M je plochý právě tehdy, když modul ${ displaystyle M _ { mathfrak {p}}}$ je byt ${ displaystyle R _ { mathfrak {p}}}$-modul pro všechny hlavní ideály ${ displaystyle { mathfrak {p}}}$ z R. Ve skutečnosti stačí zkontrolovat druhou podmínku pouze pro maximální ideály, na rozdíl od všech hlavních ideálů. Toto tvrzení snižuje otázku rovinnosti na případ (komutativních) lokálních kruhů.

Li R je místní (komutativní) kruh a buď M je definitivně generován nebo maximální ideál R je nilpotentní (např artinianský místní prsten ) pak lze standardní implikaci „free implies flat“ obrátit: v tomto případě M je plochý, pokud a jen pokud je zdarma.^[6]

The místní kritérium pro rovinnost uvádí:^[7]

Nechat R být místním noetherianským kruhem, S místní noetherian R-algebra s ${ displaystyle { mathfrak {m}} _ {R} S podmnožina { mathfrak {m}} _ {S}}$, a M konečně vygenerovaný S-modul. Pak M je naplocho R kdyby a jen kdyby ${ displaystyle operatorname {Tor} _ {1} ^ {R} (M, R / { mathfrak {m}} _ {R}) = 0.}$

To je důležité S nemusí být konečný R a musíme vzít v úvahu pouze maximální ideál R místo libovolného ideálu R.

Další kritérium je také užitečné pro testování rovinnosti:^[8]

Nechat R, S být jako v místním kritériu pro rovinnost. Převzít S je Cohen – Macaulay a R je pravidelný. Pak S je naplocho R kdyby a jen kdyby ${ displaystyle dim S = dim R + dim S / { mathfrak {m}} _ {R} S.}$

Věrně homomorfismus plochého prstence

Nechat A být prsten (předpokládá se, že v této části bude komutativní) a B an A-algebra tj. kruhový homomorfismus ${ displaystyle f: A až B}$. Pak B má strukturu A-modul. Pak B je prý plochý A (resp. věrně A) pokud je plochý (resp. věrně plochý) jako A-modul.

Existuje základní charakteristika věrně homomorfismu plochého prstence: daný homomorfismus plochého prstence ${ displaystyle f: A až B}$, následující jsou ekvivalentní.

1. ${ displaystyle f}$ je věrně plochá.
2. Pro každý maximální ideál ${ displaystyle { mathfrak {m}}}$ z ${ displaystyle A}$, ${ displaystyle { mathfrak {m}} B neq B.}$
3. Li ${ displaystyle N neq 0}$ je nenulová ${ displaystyle A}$- tedy modul ${ displaystyle N otimes _ {A} B neq 0.}$
4. Každý hlavní ideál A je inverzní obraz pod F nejlepšího ideálu v B. Jinými slovy, indukovaná mapa ${ displaystyle f ^ {*}: operatorname {Spec} (B) to operatorname {Spec} (A)}$ je surjektivní.
5. A je čistý podřetězec z B (zejména podřetězec); zde znamená „čistý podřetězec“ to ${ displaystyle N to N otimes _ {A} B}$ je injekční pro každého ${ displaystyle A}$-modul ${ displaystyle N}$.^[9]

Podmínka 2 znamená, že plochý lokální homomorfismus mezi místními kruhy je věrně plochý. Z podmínky 5 vyplývá, že ${ displaystyle I = IB cap A}$ pro každý ideál ${ displaystyle I podmnožina A}$ (vzít ${ displaystyle N = A / I}$); zejména pokud ${ displaystyle B}$ je tedy noetherovský prsten ${ displaystyle A}$ je noetherovský prsten.

Podmínku 4 lze uvést v následující posílené formě: ${ displaystyle operatorname {Spec} (B) na operatorname {Spec} (A)}$ je ponorný: topologie ${ displaystyle operatorname {specifikace} (A)}$ je kvocient topologie z ${ displaystyle operatorname {specifikace} (B)}$ (jedná se o zvláštní případ skutečnosti, že tuto vlastnost má věrně plochý kvazi-kompaktní morfismus schémat.^[10]) Srovnává se s integrální rozšíření integrálně uzavřené domény. Viz také plochý morfismus # Vlastnosti plochých morfismů pro další informace.

Zde je jedna charakteristika věrně plochého homomorfismu pro ne-nutně plochý homomorfismus. Vzhledem k injekčnímu místnímu homomorfismu ${ displaystyle (A, { mathfrak {m}}) hookrightarrow (B, { mathfrak {n}})}$ takhle ${ displaystyle { mathfrak {m}} B}$ je ${ displaystyle { mathfrak {n}}}$-primární ideál, ${ displaystyle A až B}$ je věrně plochá právě tehdy, když věta přechodu drží za to; tj. pro každého ${ displaystyle { mathfrak {m}}}$-primární ideál ${ displaystyle Q}$ z ${ displaystyle A}$, ${ displaystyle operatorname {délka} _ {B} (B / QB) = operatorname {délka} _ {B} (B / { mathfrak {m}} B) operatorname {délka} _ {A} (A / Q).}$^[11]

Příklad. Pro prsten ${ displaystyle A, A až A [x]}$ je věrně plochá. Obecněji, an ${ displaystyle A}$-algebra to je volný, uvolnit kladné hodnosti jako ${ displaystyle A}$-modul je věrně plochý. Tedy například pro monický polynom ${ displaystyle f v A [t]}$, zahrnutí ${ displaystyle A hookrightarrow A [t] / (f)}$ je věrně plochá.

Příklad. Nechat ${ displaystyle A}$ být prsten a ${ displaystyle f_ {1}, ldots, f_ {r}}$ prvky v něm. Pak tyto prvky generují jednotku ideální ${ displaystyle (1)}$ z ${ displaystyle A}$ kdyby a jen kdyby

${ displaystyle A až B = prod _ {i} A [f_ {i} ^ {- 1}]}$

je věrně plochý, protože lokalizace jsou ploché, jejich přímé součty jsou pak ploché a

${ displaystyle operatorname {Spec} B = bigcup _ {i} operatorname {Spec} A [f_ {i} ^ {- 1}] to operatorname {Spec} A}$

je surjective právě tehdy, když prvky generují ideální jednotku.^[12]

Pro daný prsten homomorfismus ${ displaystyle f: A až B,}$ existuje přidružený komplex zvaný Amitsurův komplex:^[13]

${ displaystyle 0 to A { nadměrné {f} { to}} B { nadměrné { delta ^ {0}} { to}} B jiné _ {A} B { nadměrné { delta ^ {1}} { to}} B otimes _ {A} B otimes _ {A} B to cdots}$

kde hraniční operátoři ${ displaystyle delta ^ {n}}$ jsou střídavé součty map získané vložením 1 na každé místo; např., ${ displaystyle delta ^ {0} (b) = b otimes 1-1 otimes b}$. Pak (Grothendieck) je tento komplex přesný, pokud ${ displaystyle f}$ je věrně plochá.

Homologická charakterizace pomocí funktorů Tor

Rovinnost lze také vyjádřit pomocí Tor funktory, levé odvozené funktory tenzorového produktu. A vlevo R-modul M je plochá právě tehdy

${ displaystyle operatorname {Tor} _ {n} ^ {R} (X, M) = 0}$ pro všechny ${ displaystyle n geq 1}$ a dobře R- moduly X).^[14]

Ve skutečnosti stačí zkontrolovat, že první termín Tor zmizel, tj. M je plochá právě tehdy

${ displaystyle operatorname {Tor} _ {1} ^ {R} (N, M) = 0}$

pro všechny R-modul N nebo, ještě přísněji, když ${ displaystyle N = R / I}$ a ${ displaystyle I podmnožina R}$ je jakýkoli konečně vygenerovaný ideál.

Pomocí funktoru Tor dlouhé přesné sekvence, pak lze snadno dokázat fakta o a krátká přesná sekvence

${ displaystyle 0 to A { nadměrné {f} { longrightarrow}} B { nadměrné {g} { longrightarrow}} C až 0}$

Li A a C jsou ploché, tak také jsou B. Také pokud B a C jsou ploché, tak také jsou A. Li A a B jsou ploché, C nemusí být obecně ploché, jak ukazuje výše uvedený příklad ${ displaystyle mathbb {Z} / n}$. Pokud však A je čistý v B a B je tedy plochý A a C jsou ploché.

Plochá rozlišení

A ploché rozlišení modulu M je rozlišení formuláře

${ displaystyle cdots do F_ {2} do F_ {1} do F_ {0} do M do 0,}$

Kde F_i jsou všechny ploché moduly. Jakékoli volné nebo projektivní rozlišení je nutně ploché rozlišení. Pro výpočet lze použít plochá rozlišení Tor funktor.

The délka konečného plochého rozlišení je první dolní index n takhle F_n je nenulová a F_i = 0 pro i > n. Pokud modul M připouští konečné ploché rozlišení, minimální délku mezi všemi konečnými plochými rozlišeními M se nazývá jeho plochý rozměr^[15] a označeno fd (M). Li M nepřipouští konečné konečné rozlišení, pak je podle konvence plochá dimenze považována za nekonečnou. Jako příklad zvažte modul M takový, že fd (M) = 0. V této situaci přesnost posloupnosti 0 → F₀ → M → 0 znamená, že šipka ve středu je izomorfismus, a tedy M sama o sobě je plochá.^[16]

V některých oblastech teorie modulů musí ploché rozlišení splňovat další požadavek, že každá mapa je plochým předobalem jádra mapy vpravo. Pro projektivní rozlišení je tato podmínka téměř neviditelná: projektivní předobal je prostě epimorfismus z projektivního modulu. Tyto myšlenky jsou inspirovány Auslanderovou prací v přibližných odhadech. Tyto myšlenky jsou také známé z běžnějšího pojmu minimální projektivní rozlišení, kde musí být každá mapa a projektivní kryt jádra mapy vpravo. Projektivní kryty však obecně nemusejí existovat, takže minimální projektivní rozlišení mají pouze omezené použití nad kruhy, jako jsou celá čísla.

Ploché kryty

Zatímco projektivní kryty modulů ne vždy existují, spekulovalo se, že u obecných prstenů by měl každý modul plochý kryt, to znamená každý modul M by byl epimorfní obraz plochého modulu F tak, že každá mapa z plochého modulu do M faktory Fa jakýkoli endomorfismus z F přes M je automoprhism. Tento domněnka o plochém krytu byl výslovně poprvé uveden v (Enochs 1981 196) chyba harv: žádný cíl: CITEREFEnochs1981 (Pomoc). Ukázalo se, že domněnka byla pravdivá, vyřešena pozitivně a dokázala ji současně L. Bican, R. El Bashir a E. Enochs.^[17] Předcházely tomu důležité příspěvky P. Eklofa, J. Trlifaje a J. Xu.

Protože ploché kryty existují pro všechny moduly na všech prstencích, může za mnoha okolností místo minimálních projektivních rozlišení nahradit minimální ploché rozlišení. Měří se odchylka plochých rozlišení od projektivních rozlišení relativní homologická algebra, a je zahrnuta v klasice, jako je (MacLane 1963 ) chyba harv: žádný cíl: CITEREFMacLane1963 (Pomoc) a v novějších pracích zaměřených na plochá rozlišení jako (Enochs a Jenda 2000 ).

V konstruktivní matematice

Ploché moduly mají v roce 2006 větší význam konstruktivní matematika, kde jsou projektivní moduly méně užitečné. Například, že všechny volné moduly jsou projektivní, je ekvivalentní plnému axiom volby, takže věty o projektivních modulech, i když se ukázaly konstruktivně, nemusí nutně platit pro volné moduly. Naproti tomu není třeba volit, aby se dokázalo, že volné moduly jsou ploché, takže věty o plochých modulech mohou stále platit.^[18]

Viz také

• Obecná plochost
• Plochý morfismus
• von Neumann pravidelný prsten - ty prsteny, nad kterými Všechno moduly jsou ploché.
• Normálně plochý prsten

Reference

• Artin, Michael (1999). „Nekomutativní prsteny“ (PDF).
• Bican, L .; El Bashir, R .; Enochs, E. (2001), „Všechny moduly mají ploché kryty“, Býk. London Math. Soc., 33 (4): 385–390, doi:10.1017 / S0024609301008104, ISSN  0024-6093, PAN  1832549
• N. Bourbaki, Komutativní algebra
• Chase, Stephen U. (1960), „Přímé produkty modulů“, Transakce Americké matematické společnosti, 97: 457–473, doi:10.2307/1993382, PAN  0120260
• Eisenbud, David (1995), Komutativní algebra, Postgraduální texty z matematiky, 150, Berlín, New York: Springer-Verlag, doi:10.1007/978-1-4612-5350-1, ISBN  978-0-387-94268-1, PAN  1322960, ISBN  978-0-387-94269-8
• Enochs, Edgar E. (1981), „Injekční a ploché kryty, obálky a resolventy“, Israel J. Math., 39 (3): 189–209, doi:10.1007 / BF02760849, ISSN  0021-2172, PAN  0636889
• Enochs, Edgar E .; Jenda, Overtoun M. G. (2000), Relativní homologická algebra, de Gruyter Expositions in Mathematics, 30, Berlín: Walter de Gruyter & Co., doi:10.1515/9783110803662, ISBN  978-3-11-016633-0, PAN  1753146
• Kunz, Ernst (1969), „Charakterizace pravidelných místních prstenců charakteristiky p", American Journal of Mathematics, 91: 772–784, doi:10.2307/2373351, PAN  0252389
• Lam, Tsit-Yuen (1999), Přednášky o modulech a kroužcích„Absolventské texty z matematiky č. 189, Berlín, New York: Springer-Verlag, doi:10.1007/978-1-4612-0525-8, ISBN  978-0-387-98428-5, PAN  1653294
• Lazard, D. (1969), „Autour de la platitude“, Bulletin de la Société Mathématique de France, 97: 81–128
• Mac Lane, Saunders (1963), Homologie„Die Grundlehren der mathematischen Wissenschaften, Bd. 114, Boston, MA: Akademický tisk, PAN  0156879
• Matsumura, Hidejuki (1970), Komutativní algebra
• Matsumura, Hideyuki (1986). Komutativní prstencová teorie. Cambridge studia pokročilé matematiky. 8. Cambridge University Press. ISBN  0-521-36764-6. PAN  0879273. Zbl  0603.13001.CS1 maint: ref = harv (odkaz)
• Mumford, David, Červená kniha odrůd a schémat
• Northcott, D. G. (1984), Multilineární algebra, Cambridge University Press, ISBN  978-0-521-26269-9 - strana 33
• Richman, Fred (1997), „Plochá dimenze, konstruktivita a Hilbertova věta o syzygy“, New Zealand Journal of Mathematics, 26 (2): 263–273, ISSN  1171-6096, PAN  1601663
• Serre, Jean-Pierre (1956), „Géométrie algébrique et géométrie analytique“, Annales de l'Institut Fourier, 6: 1–42, doi:10,5802 / aif.59, ISSN  0373-0956, PAN  0082175