Skupinový prsten - Group ring

v algebra, a skupinové vyzvánění je bezplatný modul a zároveň a prsten, postavené přirozeným způsobem z libovolného daného kruhu a libovolného daného skupina. Jako volný modul je jeho prsten skalárů daný prsten a jeho základ je jedna k jedné s danou skupinou. Jako prsten je jeho zákonem sčítání zákon volného modulu a jeho násobení rozšiřuje „o linearitu“ daný zákon skupiny na základě. Méně formálně je skupinový kruh zevšeobecněním dané skupiny tak, že se ke každému prvku skupiny připojí „váhový faktor“ z daného kruhu.

Skupinový kruh se také označuje jako a skupinová algebra, protože je to skutečně algebra přes daný prsten. Skupinová algebra nad polem má další strukturu a Hopfova algebra; v tomto případě se tomu říká a skupina Hopfova algebra.

Aparát skupinových kruhů je zvláště užitečný v teorii skupinové reprezentace.

Definice

Nechat G být skupina, psaná multiplikativně, a nechat R ložisko. Skupinový kruh G přes R, což budeme označovat R[G] (nebo jednoduše RG), je sada mapování F : G → R z konečná podpora,^[1] kde modul skalární součin αf skalární α v R a vektor (nebo mapování) F je definován jako vektor ${ displaystyle x mapsto alpha cdot f (x)}$ a součet skupin modulů dvou vektorů F a G je definován jako vektor ${ Displaystyle x mapsto f (x) + g (x)}$ . Chcete-li otočit skupinu aditiv R[G] do kruhu, definujeme produkt F a G být vektorem

{ Displaystyle x mapsto sum _ {uv = x} f (u) g (v) = sum _ {u in G} f (u) g (u ^ {- 1} x).}

Součet je legitimní, protože F a G jsou konečné podpory a kruhové axiomy jsou snadno ověřitelné.

Používají se některé variace v notaci a terminologii. Zejména mapování jako F : G → R jsou někdy psány jako takzvané formální lineární kombinace prvků G, s koeficienty v R":^[2]

{ displaystyle sum _ {g v G} f (g) g,}

nebo jednoduše

{ displaystyle sum _ {g v G} f_ {g} g,}

kde to nezpůsobuje zmatek.^[1]

Příklady

1. Nechte G = C₃, cyklická skupina objednávky 3, s generátorem ${ displaystyle a}$ a prvek identity 1_G. Prvek r z C[G] lze napsat jako

{ displaystyle r = z_ {0} 1_ {G} + z_ {1} a + z_ {2} a ^ {2} ,}

kde z₀, z₁ a z₂ jsou v C, komplexní čísla. To je to samé jako a polynomiální kruh v proměnné ${ displaystyle a}$ takhle ${ displaystyle a ^ {3} = a ^ {0} = 1}$ tj. C[G] je izomorfní vůči kruhu C[ ${ displaystyle a}$ ]/ ${ displaystyle (a ^ {3} -1)}$ .

Psaní jiného prvku s tak jako ${ displaystyle s = w_ {0} 1_ {G} + w_ {1} a + w_ {2} a ^ {2}}$ , jejich součet je

{ displaystyle r + s = (z_ {0} + w_ {0}) 1_ {G} + (z_ {1} + w_ {1}) a + (z_ {2} + w_ {2}) a ^ {2 } ,}

a jejich produkt je

{ displaystyle rs = (z_ {0} w_ {0} + z_ {1} w_ {2} + z_ {2} w_ {1}) 1_ {G} + (z_ {0} w_ {1} + z_ { 1} w_ {0} + z_ {2} w_ {2}) a + (z_ {0} w_ {2} + z_ {2} w_ {0} + z_ {1} w_ {1}) a ^ {2} .}

Všimněte si, že prvek identity 1_G z G indukuje kanonické vložení prstence koeficientu (v tomto případě C) do C[G]; avšak přísně vzato multiplikativní prvek identity C[G] je 1⋅1_G kde první 1 pochází z C a druhý z G. Aditivní prvek identity je nula.

Když G je nekomutativní skupina, je třeba dávat pozor na zachování pořadí prvků skupiny (a ne náhodou je dojíždět) při vynásobení výrazů.

2. Jiným příkladem je příklad Laurentovy polynomy přes prsten R: nejde o nic víc nebo méně než skupinový kruh skupiny nekonečná cyklická skupina Z přes R.

3. Nechte Q být čtveřice skupina s prvky ${ displaystyle {e, { bar {e}}, i, { bar {i}}, j, { bar {j}}, k, { bar {k}} }}$ . Zvažte skupinový kruh RQ, kde R je množina reálných čísel. Libovolný prvek tohoto skupinového kruhu má tvar

{ displaystyle x_ {1} cdot e + x_ {2} cdot { bar {e}} + x_ {3} cdot i + x_ {4} cdot { bar {i}} + x_ {5 } cdot j + x_ {6} cdot { bar {j}} + x_ {7} cdot k + x_ {8} cdot { bar {k}}}

kde ${ displaystyle x_ {i}}$ je skutečné číslo.

Násobení, stejně jako v jakémkoli jiném skupinovém kruhu, je definováno na základě skupinové operace. Například,

{ displaystyle { begin {aligned} { big (} 3 cdot e + { sqrt {2}} cdot i { big)} { big (} { frac {1} {2}} cdot { bar {j}} { big)} & = (3 cdot e) ({ frac {1} {2}} cdot { bar {j}}) + ({ sqrt {2}} cdot i) ({ frac {1} {2}} cdot { bar {j}}) & = { frac {3} {2}} cdot { big (} (e) ( { bar {j}}) { big)} + { frac { sqrt {2}} {2}} cdot { big (} (i) ({ bar {j}}) { big )} & = { frac {3} {2}} cdot { bar {j}} + { frac { sqrt {2}} {2}} cdot k end {zarovnáno}}. }

Všimněte si, že RQ není stejný jako Hamilton čtveřice přes R. Důvodem je, že Hamiltonovy čtveřice uspokojují další vztahy v kruhu, jako např ${ displaystyle -1 cdot i = -i}$ , zatímco ve skupinovém kruhu RQ, ${ displaystyle -1 cdot i}$ se nerovná ${ displaystyle 1 cdot { bar {i}}}$ . Byt více specifický, RQ má rozměr 8 jako skutečný vektorový prostor, zatímco Hamiltonovy čtveřice mají rozměr 4 jako a skutečný vektorový prostor.

Některé základní vlastnosti

Pomocí 1 označujeme multiplikativní identitu prstenu Ra označující jednotku skupiny číslem 1_G, prsten R[G] obsahuje podřetězec isomorfní na Ra jeho skupina invertibilních prvků obsahuje podskupinu isomorfní s G. Za zvážení funkce indikátoru z {1_G}, což je vektor F definován

{ displaystyle f (g) = 1 cdot 1_ {G} + součet _ {g not = 1_ {G}} 0 cdot g = mathbf {1} _ { {1_ {G} }} (g) = { begin {cases} 1 & g = 1_ {G} 0 & g neq 1_ {G} end {cases}},}

množina všech skalárních násobků F je podřetězec z R[G] izomorfní s R. A pokud mapujeme každý prvek s z G na indikátorovou funkci {s}, což je vektor F definován

{ displaystyle f (g) = 1 cdot s + součet _ {g not = s} 0 cdot g = mathbf {1} _ { {s }} (g) = { start {případů} 1 & g = s 0 & g neq s end {případy}}}

výsledné mapování je injektivní skupinový homomorfismus (s ohledem na násobení, ne sčítání, v R[G]).

Li R a G jsou komutativní (tj. R je komutativní a G je abelianská skupina ), R[G] je komutativní.

Li H je podskupina z G, pak R[H] je podřízený z R[G]. Podobně, pokud S je podřetězec z R, S[G] je podřetězec R[G].

Pokud je to pořadí skupiny G je přísně větší než 1; |G|> 1 tedy R[G] vždy nulové dělitele. Zvažte například prvek G z G objednávky |G|> 1. Pak 1 - G je nulový dělitel. Nechť |G| = m >1.

{ displaystyle (1-g) (1 + g + ... + g ^ {m-1}) = 1-g ^ {m} = 1-1 = 0}

Zvažte například skupinový kruh Z[S₃] a prvek objednávky 3 G= (123). V tomto případě,

{ displaystyle (1- (123)) (1+ (123) + (132)) = 1- (123) ^ {3} = 1-1 = 0}

Seskupte algebru nad konečnou skupinu

Skupinové algebry se přirozeně vyskytují v teorii skupinové reprezentace z konečné skupiny. Skupinová algebra K.[G] nad polem K. je v podstatě skupinový kruh s polem K. místo prstenu. Jako množinový a vektorový prostor je to volný vektorový prostor na G přes pole K.. To je pro X v K.[G],

{ displaystyle x = součet _ {g v G} a_ {g} g.}

The algebra struktura na vektorovém prostoru je definována pomocí násobení ve skupině:

{ displaystyle g cdot h = gh,}

kde nalevo, G a h označují prvky skupinové algebry, zatímco násobení vpravo je skupinová operace (označená juxtapozicí).

Protože výše uvedené násobení může být matoucí, lze také napsat základní vektory z K.[G] tak jako E_G (namísto G), v takovém případě je násobení zapsáno jako:

{ displaystyle e_ {g} cdot e_ {h} = e_ {gh}.}

Interpretace jako funkce

Myslet na volný vektorový prostor tak jako K.-hodnotené funkce na G, násobení algebry je konvoluce funkcí.

Zatímco skupinová algebra a konečný skupinu lze identifikovat s prostorem funkcí ve skupině, pro nekonečnou skupinu se liší. Skupinová algebra, skládající se z konečný součty, odpovídá funkcím ve skupině, pro které mizí definitivně mnoho bodů; topologicky (pomocí diskrétní topologie ), odpovídají funkcím s kompaktní podpora.

Skupinová algebra K.[G] a prostor funkcí K.^G : = Hom (G, K.) jsou dvojí: daný prvek skupinové algebry

{ displaystyle x = součet _ {g v G} a_ {g} g}

a funkce ve skupině F : G → K. tyto páry dát prvek K. přes

{ displaystyle (x, f) = součet _ {g v G} a_ {g} f (g),}

což je dobře definovaný součet, protože je konečný.

Pravidelné zastoupení

Skupinová algebra je algebra nad sebou; pod korespondencí zastoupení přes R a R[G] moduly, to je pravidelné zastoupení skupiny.

Psáno jako reprezentace, je to reprezentace G ↦ ρ_G s akcí danou ${ displaystyle rho (g) cdot e_ {h} = e_ {gh}}$ nebo

{ displaystyle rho (g) cdot r = součet _ {h v G} k_ {h} rho (g) cdot e_ {h} = součet _ {h v G} k_ {h} e_ {gh}.}

Vlastnosti

Dimenze vektorového prostoru K.[G] se rovná počtu prvků ve skupině. Pole K. se běžně považuje za komplexní čísla C nebo skutečné R, takže jeden diskutuje o skupinových algebrách C[G] nebo R[G].

Skupinová algebra C[G] konečné skupiny přes komplexní čísla je a polojednoduchý prsten. Tento výsledek, Maschkeova věta, nám umožňuje porozumět C[G] jako konečný produkt z maticové kroužky se záznamy v C.

Reprezentace skupinové algebry

Brát K.[G] být abstraktní algebrou, lze požádat o konkrétní reprezentace algebry nad vektorovým prostorem PROTI. Taková reprezentace

{ displaystyle { tilde { rho}}: K [G] rightarrow { mbox {End}} (V).}

je alombraický homomorfismus od skupinové algebry k množině endomorfismy na PROTI. Brát PROTI být abelianská skupina, s přidáním skupiny daným přidáním vektoru, je taková reprezentace ve skutečnosti a vlevo, odjet K.[G]-modul nad abelianskou skupinou PROTI. To je ukázáno níže, kde je potvrzen každý axiom modulu.

Výběr r ∈ K.[G] aby

{ displaystyle { tilde { rho}} (r) v { mbox {End}} (V).}

Pak ${ displaystyle { tilde { rho}} (r)}$ je v tom homomorfismus abelianských skupin

{ displaystyle { tilde { rho}} (r) cdot (v_ {1} + v_ {2}) = { tilde { rho}} (r) cdot v_ {1} + { tilde { rho}} (r) cdot v_ {2}}

pro všechny proti₁, proti₂ ∈ PROTI. Dále je třeba poznamenat, že množina endomorfismů abelianské skupiny je endomorfismus prsten. Zastoupení ${ displaystyle { tilde { rho}}}$ je kruhový homomorfismus, v tom, který má

{ displaystyle { tilde { rho}} (r + s) cdot v = { tilde { rho}} (r) cdot v + { tilde { rho}} (s) cdot v}

pro dva r, s ∈ K.[G] a proti ∈ PROTI. Podobně při násobení

{ displaystyle { tilde { rho}} (rs) cdot v = { tilde { rho}} (r) cdot { tilde { rho}} (s) cdot v.}

Nakonec jeden má, že jednotka je mapována na identitu:

{ displaystyle { tilde { rho}} (1) cdot v = v}

kde 1 je multiplikativní jednotka K.[G]; to je

{ displaystyle 1 = e_ {e}}

je vektor odpovídající prvku identity E v G.

Ukazují to poslední tři rovnice ${ displaystyle { tilde { rho}}}$ je kruhový homomorfismus z K.[G] bráno jako skupinový kruh, k endomorfickému kruhu. První identita ukázala, že jednotlivé prvky jsou skupinové homomorfismy. Tedy reprezentace ${ displaystyle { tilde { rho}}}$ je levice K.[G] -modul nad abelianskou skupinou PROTI.

Všimněte si, že vzhledem k obecnému K.[G] -modul, je indukována struktura vektorového prostoru PROTI, v tom má další axiom

{ displaystyle { tilde { rho}} (ar) cdot v_ {1} + { tilde { rho}} (br) cdot v_ {2} = a { tilde { rho}} (r ) cdot v_ {1} + b { tilde { rho}} (r) cdot v_ {2} = { tilde { rho}} (r) cdot (av_ {1} + bv_ {2} )}

pro skalární A, b ∈ K..

Libovolné zastoupení skupiny

{ displaystyle rho: G rightarrow { mbox {Aut}} (V),}

s PROTI vektorový prostor nad polem K., lze rozšířit na reprezentaci algebry

{ displaystyle { tilde { rho}}: K [G] rightarrow { mbox {End}} (V),}

jednoduše tím, že to necháte ${ displaystyle { tilde { rho}} (e_ {g}) = rho (g)}$ a lineárně se rozšiřující. Reprezentace skupiny tedy přesně odpovídají reprezentacím algebry, a tak v určitém smyslu je mluvení o jedné stejné jako mluvení o druhé.

Střed skupinové algebry

The centrum skupinové algebry je sada prvků, které dojíždějí se všemi prvky skupinové algebry:

{ displaystyle mathrm {Z} (K [G]): = vlevo {z v K [G]: celkem r v K [G], zr = rz vpravo }.}

Střed se rovná množině třídní funkce, to je sada prvků, které jsou konstantní na každé třídě konjugace

{ displaystyle mathrm {Z} (K [G]) = vlevo { součet _ {g v G} a_ {g} g: pro všechny g, h v G, a_ {g} = a_ { h ^ {- 1} gh} doprava }.}

Li K. = C, množina neredukovatelná postavy z G tvoří ortonormální základ Z (K.[G]) s ohledem na vnitřní produkt

{ displaystyle left langle sum _ {g in G} a_ {g} g, sum _ {g in G} b_ {g} g right rangle = { frac {1} {| G |}} sum _ {g v G} { bar {a}} _ {g} b_ {g}.}

Skupina zazvoní nad nekonečnou skupinou

Mnohem méně je známo v případě, kdy G je spočetně nekonečný nebo nespočetný, a toto je oblast aktivního výzkumu.^[3] Případ kde R je pole komplexních čísel je pravděpodobně nejlépe studované. V tomto případě, Irving Kaplansky dokázal, že pokud A a b jsou prvky C[G] s ab = 1, pak ba = 1. Zda je to pravda, pokud R je pole pozitivních charakteristik zůstává neznámé.

Dlouholetá domněnka o Kaplanském (~ 1940) říká, že pokud G je skupina bez kroucení, a K. je pole, pak skupinový kruh K.[G] nemá nic nepodstatného nulové dělitele. Tato domněnka je ekvivalentní K.[G] nemá nic netriviálního nilpotents za stejných hypotéz pro K. a G.

Ve skutečnosti podmínka, že K. je pole lze uvolnit na jakýkoli prsten, který lze vložit do integrální doména.

Domněnka zůstává otevřená v plné obecnosti, nicméně bylo prokázáno, že některé speciální případy skupin bez kroucení splňují domněnku nulového dělitele. Tyto zahrnují:

Unikátní skupiny produktů (např. objednatelné skupiny, zejména skupiny zdarma )
Základní přístupné skupiny (např. prakticky abelianské skupiny )
Difúzní skupiny - zejména skupiny, na které působí izometricky volně R-stromy a základní skupiny povrchových skupin s výjimkou základních skupin přímých součtů jedné, dvou nebo tří kopií projektivní roviny.

Případ G být topologická skupina je podrobněji rozebrán v článku skupinová algebra lokálně kompaktní skupiny.

Zastoupení skupinového kruhu

Modul M přes R[G] je pak stejný jako a lineární reprezentace z G přes pole R. Neexistuje žádný zvláštní důvod k omezení R být tady polem. Klasické výsledky však byly získány jako první, když R je komplexní číslo pole a G je konečná skupina, takže tento případ si zaslouží zvláštní pozornost. Ukázalo se, že R[G] je polojednoduchý prsten, za těchto podmínek, s hlubokými důsledky pro reprezentace konečných skupin. Obecněji, kdykoli charakteristický pole R nerozděluje pořadí konečné skupiny G, pak R[G] je poloviční (Maschkeova věta ).

Když G je konečný abelianská skupina, skupinový kruh je komutativní a jeho struktura je snadno vyjádřitelná kořeny jednoty. Když R je pole charakteristik pa prvočíslo p rozdělí pořadí konečné skupiny G, pak je skupinový kruh ne polojediný: má nenulovou hodnotu Jacobson radikální, a to dává odpovídající předmět teorie modulární reprezentace svůj vlastní, hlubší charakter.

Teorie kategorií

Sousední

Kategoricky, konstrukce skupinového kruhu je vlevo adjoint doskupina jednotek "; následující funktory jsou adjunkční pár:

{ displaystyle R [-] colon mathbf {Grp} to R mathbf {{ text {-}} Alg}}

{ displaystyle (-) ^ { times} dvojtečka R mathbf {{ text {-}} Alg} to mathbf {Grp}}

kde ${ displaystyle R [-]}$ převezme skupinu do skupinového kruhu R, a ${ displaystyle (-) ^ { times}}$ bere R-algebra do své skupiny jednotek.

Když R = Z, toto dává adjunkci mezi kategorie skupin a kategorie prstenů a jednotka adjunkce vezme skupinu G do skupiny, která obsahuje banální jednotky: G × {±1} = {±G}. Skupinové kruhy obecně obsahují netriviální jednotky. Li G obsahuje prvky A a b takhle ${ displaystyle a ^ {n} = 1}$ a b se nenormalizuje ${ displaystyle langle a rangle}$ pak čtverec

{ displaystyle x = (a-1) b left (1 + a + a ^ {2} + ... + a ^ {n-1} right)}

je tedy nula ${ displaystyle (1 + x) (1-x) = 1}$ . Prvek 1 + X je jednotka nekonečného řádu.

Univerzální vlastnictví

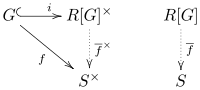
Výše uvedené spojení vyjadřuje univerzální vlastnost skupinových kruhů.^[1]^[4] Nechat R být (komutativní) prsten, ať G být skupina a nechat S být R-algebra. Pro jakýkoli skupinový homomorfismus ${ displaystyle f: G až S ^ { times}}$ existuje jedinečný R-algebra homomorfismus ${ displaystyle { overline {f}}: R [G] na S}$ takhle ${ displaystyle { overline {f}} circ i = f}$ kde i je zahrnutí

{ displaystyle { begin {zarovnáno} i: G & longrightarrow R [G] g & longmapsto 1_ {R} g end {zarovnáno}}}

Jinými slovy, ${ displaystyle { overline {f}}}$ je jedinečný homomorfismus, který umožňuje dojíždění následujícího diagramu:

Jakýkoli jiný prsten splňující tuto vlastnost je kanonicky izomorfní se skupinovým kruhem.

Zobecnění

Skupinová algebra se zobecňuje na monoidní prsten a odtud do kategorie algebra, jehož dalším příkladem je výskytová algebra.

Filtrace

Pokud má skupina a délková funkce - například pokud existuje výběr generátorů a jeden vezme slovo metrické, jako v Skupiny coxeterů - poté se skupinový kruh změní na filtrovaná algebra.

Viz také

Teorie reprezentace

Teorie kategorií

Poznámky

^ ^A ^b ^C Polcino & Sehgal (2002), s. 131.
^ Polcino & Sehgal (2002), s. 129 a 131.
^ Passman, Donald S. (1976). „Co je to skupinový kruh?“. Amer. Matematika. Měsíční. 83: 173–185. doi:10.2307/2977018.
^ "skupinová algebra v nLab". ncatlab.org. Citováno 2017-11-01.

Reference

A. A. Bovdi (2001) [1994], "Skupinová algebra", Encyclopedia of Mathematics, Stiskněte EMS
Milies, César Polcino; Sehgal, Sudarshan K. Úvod do skupinových kruhů. Algebry a aplikace, svazek 1. Springer, 2002. ISBN 978-1-4020-0238-0
Charles W. Curtis, Irving Reiner. Teorie reprezentace konečných grup a asociativních algeber, Mezivědní (1962)
D.S. Passman, Algebraická struktura skupinových kruhů, Wiley (1977)

[Polcino-1] A ^b ^C Polcino & Sehgal (2002), s. 131.

[2] Polcino & Sehgal (2002), s. 129 a 131.

[3] Passman, Donald S. (1976). „Co je to skupinový kruh?“. Amer. Matematika. Měsíční. 83: 173–185. doi:10.2307/2977018.

[4] "skupinová algebra v nLab". ncatlab.org. Citováno 2017-11-01.

[1]

[2]

[3]

[4]