Základní věta o Galoisově teorii - Fundamental theorem of Galois theory

tento článek ne uvést žádný Zdroje. Prosím pomozte vylepšit tento článek podle přidávání citací ke spolehlivým zdrojům. Zdroj bez zdroje může být napaden a odstraněn. Najít zdroje: „Základní věta o Galoisově teorii“  – zprávy  · noviny  · knihy  · učenec  · JSTOR (Září 2015) (Zjistěte, jak a kdy odstranit tuto zprávu šablony)

v matematika, základní věta o Galoisově teorii je výsledek, který popisuje strukturu určitých typů rozšíření pole ve vztahu k skupiny. Dokázal to Évariste Galois v jeho vývoji Galoisova teorie.

V nejzákladnější formě věta tvrdí, že vzhledem k rozšíření pole E/F to je konečný a Galois, tady je osobní korespondence mezi jeho mezilehlými poli a podskupiny jeho Galoisova skupina. (Střední pole jsou pole K. uspokojující F ⊆ K. ⊆ E; jsou také nazýváni dílčí rozšíření z E/F.)

Výslovný popis korespondence

U konečných rozšíření lze korespondenci popsat explicitně následovně.

• Pro jakoukoli podskupinu H Gal (E/F), korespondence pevné pole, označeno E^H, je soubor těchto prvků E které jsou opraveny každým automorfismus v H.
• Pro jakékoli mezilehlé pole K. z E/F, odpovídající podskupina je Aut (E/K.), tj. soubor těchto automorfismů v Gal (E/F) které opravují všechny prvky K..

Základní věta říká, že tato korespondence je korespondence jedna k jedné, pokud (a pouze pokud) E/F je Galoisovo rozšíření Například nejvyšší pole E odpovídá triviální podskupina Gal (E/F) a základní pole F odpovídá celku skupina Gal (E/F).

Zápis Gal (E/F) se používá pouze pro Galois rozšíření. Li E/F je Galois, pak Gal (E/F) = Aut (E/F). Li E/F není Galois, pak "korespondence" dává pouze injekční (ale ne surjektivní ) mapa z ${ displaystyle {{ text {podskupiny Aut}} (E / F) }}$ na ${ displaystyle {{ text {podpole}} E / F }}$, a surjektivní (ale nikoli injektivní) mapa v opačném směru. Zejména pokud E/F tedy není Galois F není pevné pole žádné podskupiny Aut (E/F).

Vlastnosti korespondence

Korespondence má následující užitečné vlastnosti.

• to je obrácení inkluze. Zahrnutí podskupin H₁ ⊆ H₂ platí pouze tehdy, pokud je zahrnuto pole E^H₁ ⊇ E^H₂ drží.
• Stupně rozšíření souvisí s objednávkami skupin způsobem, který je konzistentní s vlastností inverze zařazení. Konkrétně pokud H je podskupina Gal (E/F), pak |H| = [E:E^H] a | Gal (E/F)|/|H| = [E^H:F].
• Pole E^H je normální rozšíření z F (nebo ekvivalentně rozšíření Galois, protože libovolné dílčí rozšíření oddělitelné rozšíření je oddělitelné) právě tehdy, H je normální podskupina Gal (E/F). V tomto případě je omezení prvků Gal (E/F) až E^H vyvolává izomorfismus mezi Gal (E^H/F) a kvocientová skupina Gal (E/F)/H.

Příklad 1

Zvažte pole

${ displaystyle K = mathbb {Q} left ({ sqrt {2}}, { sqrt {3}} right) = left [ mathbb {Q} ({ sqrt {2}}) vpravo] ({ sqrt {3}}).}$

Od té doby K. je nejprve určen sousedním √2, pak √3, každý prvek K. lze napsat jako:

${ displaystyle left (a + b { sqrt {2}} right) + left (c + d { sqrt {2}} right) { sqrt {3}}, qquad a, b, c, d in mathbb {Q}.}$

Její skupina Galois ${ displaystyle G = { text {Gal}} (K / mathbb {Q})}$ lze určit zkoumáním automorfismů K. který opravit A. Každý takový automorfismus musí poslat √2 buď √2 nebo –√2a musí odeslat √3 buď √3 nebo –√3 protože permutace ve skupině Galois mohou permutovat pouze kořeny neredukovatelného polynomu. Předpokládejme to F výměny √2 a –√2, tak

${ displaystyle f left ((a + b { sqrt {2}}) + (c + d { sqrt {2}}) { sqrt {3}} right) = (ab { sqrt {2 }}) + (cd { sqrt {2}}) { sqrt {3}} = ab { sqrt {2}} + c { sqrt {3}} - d { sqrt {6}},}$

a G výměny √3 a –√3, tak

${ displaystyle g left ((a + b { sqrt {2}}) + (c + d { sqrt {2}}) { sqrt {3}} right) = (a + b { sqrt {2}}) - (c + d { sqrt {2}}) { sqrt {3}} = a + b { sqrt {2}} - c { sqrt {3}} - d { sqrt {6}}.}$

To jsou zjevně automorfismy K.. Existuje také automatorfismus identity E který nic nemění, a složení F a G který mění značky na oba radikály:

${ displaystyle (fg) left ((a + b { sqrt {2}}) + (c + d { sqrt {2}}) { sqrt {3}} right) = (ab { sqrt {2}}) - (cd { sqrt {2}}) { sqrt {3}} = ab { sqrt {2}} - c { sqrt {3}} + d { sqrt {6}} .}$

Proto,

${ displaystyle G = left {1, f, g, fg right },}$

a G je isomorfní s Kleinova čtyřčlenná skupina. Má pět podskupin, z nichž každá odpovídá pomocí věty podpoli K..

• Triviální podskupina (obsahující pouze prvek identity) odpovídá všem K..
• Celá skupina G odpovídá základnímu poli ${ displaystyle mathbb {Q}.}$
• Podskupina se dvěma prvky {1, F} odpovídá podpole ${ displaystyle mathbb {Q} ({ sqrt {3}}),}$ od té doby F opravy √3.
• Podskupina se dvěma prvky {1, G} odpovídá podpole ${ displaystyle mathbb {Q} ({ sqrt {2}}),}$ od té doby znovu G opravy √2.
• Podskupina se dvěma prvky {1, fg} odpovídá podpole ${ displaystyle mathbb {Q} ({ sqrt {6}}),}$ od té doby fg opravy √6.

Příklad 2

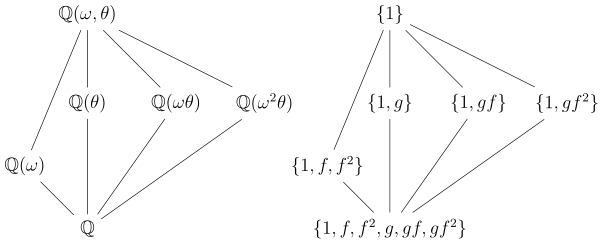
Toto je nejjednodušší případ, kdy skupina Galois není abelian.

Zvažte rozdělení pole K. polynomu ${ displaystyle x ^ {3} -2}$ přes ${ displaystyle mathbb {Q};}$ to je ${ displaystyle K = mathbb {Q} ( omega, theta)}$ kde θ je kořenová kostka 2, a ω je kořenová kostka 1 (ale ne 1 sama). Například, když si představíme K. abychom byli uvnitř pole komplexních čísel, můžeme vzít θ jako skutečný kořen krychle 2 a ω jako

${ displaystyle omega = { frac {-1} {2}} + i { frac { sqrt {3}} {2}}.}$

Je možné ukázat, že skupina Galois ${ displaystyle G = { text {Gal}} (K / mathbb {Q})}$ má šest prvků a je izomorfní se skupinou permutací tří objektů. Je generován (například) dvěma automorfizmy, řekněme F a G, které jsou určeny jejich účinkem na θ a ω,

${ displaystyle f ( theta) = omega theta, quad f ( omega) = omega,}$

${ displaystyle g ( theta) = theta, quad g ( omega) = omega ^ {2},}$

a pak

${ displaystyle G = left {1, f, f ^ {2}, g, gf, gf ^ {2} right }.}$

Podskupiny G a odpovídající podpole jsou následující:

• Jako obvykle celá skupina G odpovídá základnímu poli ${ displaystyle mathbb {Q}}$ a triviální skupina {1} odpovídá celému poli K..
• Existuje jedinečná podskupina řádu 3, jmenovitě ${ displaystyle {1, f, f ^ {2} }.}$ Odpovídající podpole je ${ displaystyle mathbb {Q} ( omega),}$ který má stupeň 2 u konce ${ displaystyle mathbb {Q}}$ (dále jen minimální polynom z ω je ${ displaystyle x ^ {2} + x + 1}$), což odpovídá skutečnosti, že podskupina má index dva dovnitř G. Tato podskupina je také normální, což odpovídá skutečnosti, že podpole je normální ${ displaystyle mathbb {Q}.}$
• Existují tři podskupiny řádu 2, jmenovitě ${ displaystyle {1, g }, {1, gf }}$ a ${ displaystyle {1, gf ^ {2} },}$ odpovídající příslušně třem podpolím ${ displaystyle mathbb {Q} ( theta), mathbb {Q} ( omega theta), mathbb {Q} ( omega ^ {2} theta).}$ Tato podpole mají 3. stupeň ${ displaystyle mathbb {Q},}$ opět odpovídá podskupinám, které mají index 3 palce G. Všimněte si, že podskupiny jsou ne normální v G, a to odpovídá skutečnosti, že podpole jsou ne Galois skončil ${ displaystyle mathbb {Q}.}$ Například, ${ displaystyle mathbb {Q} ( theta)}$ obsahuje pouze jeden kořen polynomu ${ displaystyle x ^ {3} -2,}$ tak to nemůže být normální přes ${ displaystyle mathbb {Q}.}$

Příklad 3

Nechat ${ displaystyle E = mathbb {Q} ( lambda)}$ být oblastí racionálních funkcí v ${ displaystyle lambda}$ a nechte

${ displaystyle G = left lbrace { lambda, { frac {1} {1- lambda}}, { frac { lambda -1} { lambda}}, { frac {1} { lambda}}, { frac { lambda} { lambda -1}}, 1- lambda} right rbrace subset { rm {Aut}} (E)}$

což je skupina ve složení, isomorfní s ${ displaystyle S_ {3}}$ (vidět: šest křížových poměrů ).Nechat ${ displaystyle F}$ být pevné pole ${ displaystyle G}$, pak ${ displaystyle { rm {Gal}} (E / F) = G}$.

Li ${ displaystyle H}$ je podskupina ${ displaystyle G}$ pak koeficienty následujícího polynomu

${ displaystyle P (T): = prod _ {h v H} (T-h) v E [T]}$

generovat pevné pole ${ displaystyle H}$. Galoisova korespondence znamená, že každé podpole ${ displaystyle E / F}$ lze konstruovat tímto způsobem. Například pokud ${ displaystyle H = { lambda, 1- lambda }}$ pak je pevné pole ${ displaystyle mathbb {Q} ( lambda (1- lambda))}$ a pokud ${ displaystyle H = { lambda, 1 / lambda }}$ pak je pevné pole ${ displaystyle mathbb {Q} ( lambda + 1 / lambda)}$. Podobně lze psát ${ displaystyle F}$, pevné pole ${ displaystyle G}$, tak jako ${ displaystyle mathbb {Q} (j),}$ kde j je j-invariantní.

Podobné příklady lze zkonstruovat pro každou z skupiny symetrie platonických pevných látek protože také mají věrné činy na projektivní linie ${ displaystyle mathbb {P} ^ {1} ( mathbb {C})}$ a tedy dál ${ displaystyle mathbb {C} (x)}$.

Aplikace

Věta klasifikuje mezilehlá pole E/F ve smyslu teorie skupin. Tento překlad mezi mezilehlými poli a podskupinami je klíčem k prokázání, že obecná kvintická rovnice není řešitelné radikály (vidět Abel – Ruffiniho věta ). Jeden nejprve určí Galoisovy skupiny radikální rozšíření (rozšíření formuláře F(α) kde α je n-tý kořen nějakého prvku F), a poté pomocí základní věty ukáže, že řešitelné rozšíření odpovídá řešitelné skupiny.

Teorie jako Kummerova teorie a teorie pole jsou založeny na základní větě.

Nekonečný případ

Vzhledem k nekonečnému algebraickému rozšíření jej můžeme stále definovat jako Galois, pokud je normální a oddělitelný. Problém, se kterým se člověk setkává v nekonečném případě, spočívá v tom, že bijekce v základní větě neplatí, protože obecně dostáváme příliš mnoho podskupin. Přesněji, pokud vezmeme jen každou podskupinu, můžeme obecně najít dvě různé podskupiny, které opravují stejné mezilehlé pole. Proto to pozměňujeme zavedením a topologie ve skupině Galois.

Nechat ${ displaystyle E / F}$ být příponou Galois (možná nekonečná) a nechat ${ displaystyle G = { text {Gal}} (E / F)}$ být Galoisovou skupinou rozšíření. Nechat

být množinou Galoisových skupin všech konečných přechodných rozšíření Galois. Všimněte si, že pro všechny ${ displaystyle i in I}$ můžeme definovat mapy ${ displaystyle varphi _ {i}: G rightarrow G_ {i}}$ podle ${ displaystyle sigma mapsto sigma _ {| L_ {i}}}$. Poté definujeme Topologie Krull na ${ displaystyle G}$ být nejslabší topologií takovou pro všechny ${ displaystyle i in I}$ mapy ${ displaystyle varphi _ {i}: G rightarrow G_ {i}}$ jsou spojité, kde je každý obdarujeme ${ displaystyle G_ {i}}$ s diskrétní topologií. Uvedeno jinak ${ displaystyle G cong varprojlim G_ {i}}$ jako inverzní limit z topologické skupiny (kde zase každý ${ displaystyle G_ {i}}$ je vybaven diskrétní topologií). To dělá ${ displaystyle G}$ A profinitní skupina (ve skutečnosti každá profinitní skupina může být realizována jako Galoisova skupina rozšíření Galois, viz například ^[1]). Všimněte si, že když ${ displaystyle E / F}$ je konečná, Krullova topologie je diskrétní topologie.

Nyní, když jsme definovali topologii na Galoisově skupině, můžeme přepracovat základní teorém pro nekonečné Galoisovo rozšíření.

Nechat ${ displaystyle { mathcal {F}}}$ označuje množinu všech konečných mezilehlých rozšíření pole ${ displaystyle E / F}$ a nechte ${ displaystyle { mathcal {C}}}$ označuje množinu všech uzavřených podskupin ${ displaystyle G = { text {Gal}} (E / F)}$ obdařen Krull topologií. Pak mezi nimi existuje bijekce ${ displaystyle { mathcal {F}}}$ a ${ displaystyle { mathcal {C}}}$ dané mapou

definován ${ displaystyle L mapsto { text {Gal}} (E / L)}$ a mapa definován ${ displaystyle N mapsto { text {Fix}} _ {E} (N): = {a v E ~ | ~ sigma (a) = a { text {pro všechny}} sigma v N }}$. Jedna důležitá věc, kterou musíte zkontrolovat, je to ${ displaystyle Phi}$ je dobře definovaná mapa, to je ono ${ displaystyle Phi (L)}$ je uzavřená podskupina ${ displaystyle G}$ pro všechny středně pokročilé. Důkaz viz například ^[1]

Reference

externí odkazy

• Média související s Základní věta o Galoisově teorii na Wikimedia Commons