Pappussova šestihranná věta - Pappuss hexagon theorem - Wikipedia

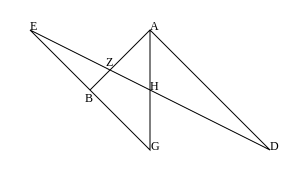
V matematice Pappusova šestihranná věta (připisováno Pappus Alexandrijský ) tvrdí, že
- vzhledem k jedné sadě kolineární bodů a další sada kolineárních bodů , pak průsečíky z čára páry a a a jsou kolineární, ležící na Pappusova linie. Tyto tři body jsou průsečíky „protilehlých“ stran šestiúhelníku .
Platí v projektivní rovina přes jakékoli pole, ale selže pro projektivní roviny nad jakýmkoli nekomutativním dělící prsten.[1] Nazývají se projektivní roviny, ve kterých platí „věta“ pappianská letadla.
Pokud někdo omezuje projektivní rovinu tak, že Pappusova linie je čára v nekonečnu, jeden dostane afinní verze Pappusovy věty zobrazené ve druhém diagramu.
Pokud je Pappusova linie a řádky mít společný bod, jeden dostane tzv málo verze Pappusovy věty[2].
The dvojí z toho věta o výskytu uvádí, že vzhledem k jedné sadě souběžné linky a další sada souběžných linek , pak řádky definované dvojicemi bodů vyplývajícími z dvojic průsečíků a a a jsou souběžné. (Souběžně znamená, že čáry procházejí jedním bodem.)
Pappusova věta je a speciální případ z Pascalova věta pro kuželovitý tvar - omezující případ když kuželovitý degeneruje do 2 přímek. Pascalova věta je zase zvláštním případem Cayley – Bacharachova věta.
The Konfigurace Pappus je konfigurace 9 řádků a 9 bodů, které se vyskytují v Pappusově větě, přičemž každý řádek splňuje 3 body a každý bod splňuje 3 řádky. Obecně platí, že čára Pappus neprochází průsečíkem a .[3] Tato konfigurace je já dvojí. Protože zejména řádky mají vlastnosti čar dvojí věty a kolineárnosti je ekvivalentem souběhu , dvojitá věta je proto stejná jako věta sama. The Leviho graf konfigurace Pappus je Pappusův graf, a bipartitní vzdálenost-pravidelná graf s 18 vrcholy a 27 hranami.
Důkaz: afinní forma

Pokud lze dokázat afinní formu výroku, je dokázána projektivní forma Pappusovy věty, protože rozšíření pappiánské roviny na projektivní rovinu je jedinečné.
Kvůli paralelitě v afinní rovině je třeba rozlišit dva případy: a . Klíčem pro jednoduchý důkaz je možnost zavedení „vhodného“ souřadnicového systému:
Případ 1: Čáry protínají se v bodě .
V tomto případě jsou zavedeny souřadnice (viz schéma). mít souřadnice .
Z rovnoběžnosti čar jeden dostane a rovnoběžnost čar výnosy . Proto linka má sklon a je rovnoběžná .
Případ 2: (malá věta).
V tomto případě jsou souřadnice zvoleny tak, že . Z paralelity a jeden dostane a , respektive, a alespoň rovnoběžnost .
Důkaz s homogenními souřadnicemi
Zvolte homogenní souřadnice pomocí
- .
Na řádcích , dána , vezměte body být
pro některé . Tři řádky jsou , takže procházejí stejným bodem kdyby a jen kdyby . Podmínka pro tři řádky a s rovnicemi projít stejným bodem je . Takže tato poslední sada tří řádků je souběžná, pokud všech ostatních osm sad je proto, že násobení je komutativní, takže . Ekvivalentně jsou kolineární.
Důkaz výše také ukazuje, že pro udržení projektivního prostoru nad dělícím prstencem je pro Pappusovu větu dostačující a nezbytné, aby dělící prsten byl (komutativní) pole. Německý matematik Gerhard Hessenberg dokázal, že Pappusova věta naznačuje Desarguesova věta.[4][5] Obecně platí, že Pappusova věta platí pro nějakou projektivní rovinu právě tehdy, pokud jde o projektivní rovinu nad komutativním polem. Projektivní roviny, ve kterých Pappusova věta neplatí, jsou Desarguesian - projektivní roviny nad nekomutativními dělícími kruhy a - nedesarguesiánská letadla.
Důkaz je neplatný, pokud stalo se kolineární. V takovém případě lze poskytnout alternativní důkaz, například pomocí jiné projektivní reference.
Duální věta
Kvůli princip duality pro projektivní roviny the dvojí věta o Pappusovi je pravda:
Pokud 6 řádků jsou voleny střídavě ze dvou tužky s centry , čáry
jsou souběžné, to znamená: mají bod společné.
Levý diagram ukazuje projektivní verzi, pravý afinní verzi, kde jsou body jsou body v nekonečnu. Pokud bod je na lince než jeden dostane „dvojí malou větu“ Pappusovy věty.

duální věta: projektivní forma

duální věta: afinní forma
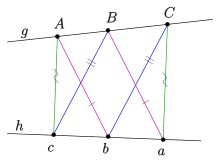
Pokud je v afinní verzi dvojího bodu „malá věta“ je také bod v nekonečnu, jeden dostane Thomsenova věta, prohlášení o 6 bodech po stranách trojúhelníku (viz obrázek). Thomsenova postava hraje zásadní roli při koordinaci axiomaticky definované projektivní roviny[6]. Důkaz o uzavření Thomsenovy postavy je zakryt výše uvedeným důkazem pro „malou větu“. Existuje však také jednoduchý přímý důkaz:
Protože tvrzení Thomsenovy věty (uzavření obrázku) používá pouze termíny připojit, protínat a paralelní, prohlášení je afinně invariantní a lze zavést takové souřadnice (viz pravé schéma). Počáteční bod posloupnosti akordů je Jeden snadno ověří souřadnice bodů uvedených v diagramu, který ukazuje: poslední bod se shoduje s prvním bodem.

Thomsenova postava (body trojúhelníku ) jako dvojitá věta o malé Pappusově větě ( je také v nekonečnu!).

Thomsenova postava: důkaz
Další výroky věty

Kromě výše uvedených charakteristik Pappusovy věty a její dvojí formy jsou ekvivalentní následující výroky:
- Pokud šest vrcholů šestiúhelníku leží střídavě na dvou přímkách, pak jsou tři průsečíky párů protilehlých stran kolineární.[7]
- Uspořádáno do matice devíti bodů (jako na obrázku a v popisu výše) a považováno za hodnotící a trvalý, pokud jsou první dva řádky a šest „diagonálních“ triád kolineární, pak je třetí řada kolineární.
- To je, pokud jsou řádky, pak to říká Pappusova věta musí být čára. Všimněte si také, že stejná maticová formulace platí pro duální formu věty, když atd. jsou trojité souběžné linky.[8]
- Vzhledem ke třem odlišným bodům na každé ze dvou odlišných linií spárujte každý bod na jedné z linií s jedním z druhé linie, poté se spojení bodů, které nejsou spárovány, setkají v (opačných) párech v bodech podél linie.[9]
- Pokud jsou dva trojúhelníky perspektivní přinejmenším dvěma různými způsoby, pak jsou perspektivní třemi způsoby.[4]
- Li a jsou souběžné a a jsou tedy souběžné a jsou souběžné.[8]
Počátky
Ve své nejstarší známé formě je Pappusova věta Propozice 138, 139, 141 a 143 knihy VII z Pappus Sbírka.[10] Jedná se o lemmy XII, XIII, XV a XVII v části knihy VII sestávající z lemmat k první ze tří knih Euklid je Porismy.
Lemata jsou dokázána z hlediska toho, co je dnes známé jako křížový poměr čtyř kolineárních bodů. Používají se tři dřívější lemata. První z nich, Lemma III, má níže uvedený diagram (který používá Pappusovo písmo s G pro Γ, D pro Δ, J pro Θ a L pro Λ).
Zde jsou tři souběžné přímky, AB, AG a AD, protínány dvěma přímkami, JB a JE, které se shodují v J. Rovněž KL je nakresleno AZ.
- KJ: JL :: (KJ: AG & AG: JL) :: (JD: GD & BG: JB).
Tyto proporce lze dnes zapsat jako rovnice:[11]
- KJ / JL = (KJ / AG) (AG / JL) = (JD / GD) (BG / JB).
Poslední složený poměr (jmenovitě JD: GD & BG: JB) je dnes známý jako křížový poměr kolineárních bodů J, G, D a B v tomto pořadí; dnes je označován (J, G; D, B). Ukázali jsme tedy, že to je nezávislé na volbě konkrétní přímky JD, která protíná tři přímky, které se shodují v A. Zejména
- (J, G; D, B) = (J, Z; H, E).
Nezáleží na tom, na kterou stranu A padá přímka JE. Zejména může být situace jako v následujícím diagramu, což je diagram pro Lemma X.
Stejně jako dříve máme (J, G; D, B) = (J, Z; H, E). Pappus to výslovně neprokazuje; ale Lemma X je konverzace, totiž, že pokud jsou tyto dva křížové poměry stejné a přímky BE a DH se protínají v A, pak body G, A a Z musí být kolineární.
To, co jsme původně ukázali, lze napsat jako (J, ∞; K, L) = (J, G; D, B), přičemž ∞ nahradí (neexistující) křižovatku JK a AG. Pappus to ukazuje ve skutečnosti v Lemmě XI, jejíž diagram má však jiné písmo:
To, co Pappus ukazuje, je DE.ZH: EZ.HD :: GB: BE, které můžeme psát jako
- (D, Z; E, H) = (∞, B; E, G).
Diagram pro Lemma XII je:
Schéma pro Lemma XIII je stejné, ale BA a DG, rozšířené, se setkávají v N. V každém případě, bereme-li v úvahu přímé přímky procházející G jako řezané třemi přímkami procházející A (a akceptující, že rovnice křížových poměrů zůstanou platné i po permutace záznamů,) máme u Lemmy III nebo XI
- (G, J; E, H) = (G, D; ∞ Z).
Vezmeme-li v úvahu přímé čáry procházející D, které jsou řezány třemi přímkami procházejícími B, máme
- (L, D; E, K) = (G, D; ∞ Z).
Tedy (E, H; J, G) = (E, K; D, L), takže pomocí Lemmy X jsou body H, M a K kolineární. To znamená, že průsečíky dvojic protilehlých stran šestiúhelníku ADEGBZ jsou kolineární.
Lemmy XV a XVII jsou takové, že pokud je bod M určen jako průsečík HK a BG, pak jsou body A, M a D kolineární. To znamená, že průsečíky dvojic protilehlých stran šestiúhelníku BEKHZG jsou kolineární.
Poznámky
- ^ Coxeter, str. 236–7
- ^ Rolf Lingenberg: Grundlagen der Geometrie, BI-Taschenbuch, 1969, s. 93
- ^ K tomu však dochází, když a jsou v perspektivní, to znamená, a jsou souběžné.
- ^ A b Coxeter 1969, str. 238
- ^ Podle (Dembowski 1968, str. 159, poznámka pod čarou 1), Hessenbergův původní důkaz Hessenberg (1905) není kompletní; nezohlednil možnost, že v konfiguraci Desargues může dojít k dalším incidentům. Kompletní důkaz poskytuje Cronheim 1953.
- ^ W. Blaschke: Projektivní geometrie, Springer-Verlag, 2013, ISBN 3034869320, S. 190
- ^ Coxeter, str. 231
- ^ A b Coxeter, str. 233
- ^ Whicher, kapitola 14
- ^ Heath (sv. II, s. 421) uvádí tato tvrzení. Poslední dva lze chápat jako konverze prvních dvou. Kline (str. 128) cituje pouze Propozici 139. Číslování propozic určuje Hultsch.
- ^ Důvodem pro použití výše uvedené notace je to, že u starověkých Řeků poměr není číslo nebo geometrický objekt. Můžeme si dnes představit poměr jako třídu ekvivalence párů geometrických objektů. Rovnost pro Řeky je také to, čemu bychom dnes mohli říkat shoda. Zejména odlišné úsečky mohou být stejné. Poměry nejsou rovnat se v tomto smyslu; ale mohou být stejný.
Reference
- Coxeter, Harold Scott MacDonald (1969), Úvod do geometrie (2. vyd.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, PAN 0123930
- Cronheim, A. (1953), „Důkaz Hessenbergovy věty“, Proceedings of the American Mathematical Society, 4 (2): 219–221, doi:10.2307/2031794, JSTOR 2031794
- Dembowski, Peter (1968), Konečné geometrie, Berlín: Springer Verlag
- Heath, Thomas (1981) [1921], Historie řecké matematiky, New York: Dover
- Hessenberg, Gerhard (1905), „Beweis des Desarguesschen Satzes aus dem Pascalschen“, Mathematische Annalen, Berlín / Heidelberg: Springer, 61 (2): 161–172, doi:10.1007 / BF01457558, ISSN 1432-1807
- Hultsch, Fridericus (1877), Pappi Alexandrini Collectionis Quae Supersunt, Berlín
- Kline, Morris (1972), Matematické myšlení od starověku po moderní dobu, New York: Oxford University Press
- Whicher, Olive (1971), Projektivní geometrie, Rudolph Steiner Press, ISBN 0-85440-245-4