v matematika , související legendární polynomy jsou kanonická řešení obecná Legendreova rovnice
( 1 − X 2 ) d 2 d X 2 P ℓ m ( X ) − 2 X d d X P ℓ m ( X ) + [ ℓ ( ℓ + 1 ) − m 2 1 − X 2 ] P ℓ m ( X ) = 0 { displaystyle (1-x ^ {2}) { frac {d ^ {2}} {dx ^ {2}}} P _ { ell} ^ {m} (x) -2x { frac {d} {dx}} P _ { ell} ^ {m} (x) + left [ ell ( ell +1) - { frac {m ^ {2}} {1-x ^ {2}}} vpravo] P _ { ell} ^ {m} (x) = 0} nebo ekvivalentně
d d X [ ( 1 − X 2 ) d d X P ℓ m ( X ) ] + [ ℓ ( ℓ + 1 ) − m 2 1 − X 2 ] P ℓ m ( X ) = 0 { displaystyle { frac {d} {dx}} vlevo [(1-x ^ {2}) { frac {d} {dx}} P _ { ell} ^ {m} (x) vpravo] + left [ ell ( ell +1) - { frac {m ^ {2}} {1-x ^ {2}}} right] P _ { ell} ^ {m} (x) = 0 } kde indexy ℓ a m (což jsou celá čísla) se označují jako stupeň a pořadí přidruženého Legendrova polynomu. Tato rovnice má nenulová řešení, která jsou nesingulární na [−1, 1], pouze pokud ℓ a m jsou celá čísla s 0 ≤ m ≤ ℓ nebo s triviálně ekvivalentními zápornými hodnotami. Když navíc m je sudé, funkce je a polynomiální . Když m je nula a celé číslo,, tyto funkce jsou identické s Legendární polynomy . Obecně platí, že když ℓ a m jsou celá čísla, běžná řešení se někdy nazývají „přidružené Legendrovy polynomy“, i když tomu tak není polynomy když m je zvláštní. Plně obecná třída funkcí s libovolnými reálnými nebo komplexními hodnotami ℓ a m jsou Legendární funkce . V takovém případě jsou parametry obvykle označeny řeckými písmeny.
The Legendre obyčejná diferenciální rovnice se často vyskytuje v fyzika a další technické obory. Zejména k tomu dochází při řešení Laplaceova rovnice (a související parciální diferenciální rovnice ) v sférické souřadnice . Přidružené Legendrovy polynomy hrají při definici zásadní roli sférické harmonické .
Definice nezáporných celočíselných parametrů ℓ a m Tyto funkce jsou označeny P ℓ m ( X ) { displaystyle P _ { ell} ^ {m} (x)} P . Jejich nejpřímější definice je v derivátech obyčejných Legendární polynomy (m ≥ 0)
P ℓ m ( X ) = ( − 1 ) m ( 1 − X 2 ) m / 2 d m d X m ( P ℓ ( X ) ) { displaystyle P _ { ell} ^ {m} (x) = (- 1) ^ {m} (1-x ^ {2}) ^ {m / 2} { frac {d ^ {m}} { dx ^ {m}}} vlevo (P _ { ell} (x) vpravo)} The (-1)m Condon – Shortleyova fáze . Někteří autoři to vynechávají. Funkce popsané v této rovnici splňují obecnou Legendrovu diferenciální rovnici s uvedenými hodnotami parametrů ℓ a m následuje diferenciace m krát Legendrova rovnice pro P ℓ :[1]
( 1 − X 2 ) d 2 d X 2 P ℓ ( X ) − 2 X d d X P ℓ ( X ) + ℓ ( ℓ + 1 ) P ℓ ( X ) = 0. { displaystyle (1-x ^ {2}) { frac {d ^ {2}} {dx ^ {2}}} P _ { ell} (x) -2x { frac {d} {dx}} P _ { ell} (x) + ell ( ell +1) P _ { ell} (x) = 0.} Navíc, protože Rodriguesův vzorec ,
P ℓ ( X ) = 1 2 ℓ ℓ ! d ℓ d X ℓ [ ( X 2 − 1 ) ℓ ] , { displaystyle P _ { ell} (x) = { frac {1} {2 ^ { ell} , ell!}} { frac {d ^ { ell}} {dx ^ { ell }}} left [(x ^ {2} -1) ^ { ell} right],} the P m ℓ
P ℓ m ( X ) = ( − 1 ) m 2 ℓ ℓ ! ( 1 − X 2 ) m / 2 d ℓ + m d X ℓ + m ( X 2 − 1 ) ℓ . { displaystyle P _ { ell} ^ {m} (x) = { frac {(-1) ^ {m}} {2 ^ { ell} ell!}} (1-x ^ {2}) ^ {m / 2} { frac {d ^ { ell + m}} {dx ^ { ell + m}}} (x ^ {2} -1) ^ { ell}.} Tato rovnice umožňuje rozšíření rozsahu m do: −ℓ ≤ m ≤ ℓ. Definice P ℓ ±m , vyplývající z tohoto výrazu substitucí ±m , jsou proporcionální. Opravdu vyrovnejte koeficienty stejné síly na levé a pravé straně
d ℓ − m d X ℓ − m ( X 2 − 1 ) ℓ = C l m ( 1 − X 2 ) m d ℓ + m d X ℓ + m ( X 2 − 1 ) ℓ , { displaystyle { frac {d ^ { ell -m}} {dx ^ { ell -m}}} (x ^ {2} -1) ^ { ell} = c_ {lm} (1-x ^ {2}) ^ {m} { frac {d ^ { ell + m}} {dx ^ { ell + m}}} (x ^ {2} -1) ^ { ell},} z toho vyplývá, že konstanta proporcionality je
C l m = ( − 1 ) m ( ℓ − m ) ! ( ℓ + m ) ! , { displaystyle c_ {lm} = (- 1) ^ {m} { frac {( ell -m)!} {( ell + m)!}},} aby
P ℓ − m ( X ) = ( − 1 ) m ( ℓ − m ) ! ( ℓ + m ) ! P ℓ m ( X ) . { displaystyle P _ { ell} ^ {- m} (x) = (- 1) ^ {m} { frac {( ell -m)!} {( ell + m)!}} P _ { ell} ^ {m} (x).} Alternativní notace V literatuře se také používají následující alternativní notace:[2]
P ℓ m ( X ) = ( − 1 ) m P ℓ m ( X ) { displaystyle P _ { ell m} (x) = (- 1) ^ {m} P _ { ell} ^ {m} (x)} Uzavřená forma Associated Legendre Polynomial lze také psát jako:
P l m ( X ) = ( − 1 ) m ⋅ 2 l ⋅ ( 1 − X 2 ) m / 2 ⋅ ∑ k = m l k ! ( k − m ) ! ⋅ X k − m ⋅ ( l k ) ( l + k − 1 2 l ) { displaystyle P_ {l} ^ {m} (x) = (- 1) ^ {m} cdot 2 ^ {l} cdot (1-x ^ {2}) ^ {m / 2} cdot součet _ {k = m} ^ {l} { frac {k!} {(km)!}} cdot x ^ {km} cdot { binom {l} {k}} { binom { frac {l + k-1} {2}} {l}}} s jednoduchými monomials a zobecněná forma binomického koeficientu .
Ortogonalita Přidružené Legendrovy polynomy nejsou obecně vzájemně ortogonální. Například, P 1 1 { displaystyle P_ {1} ^ {1}} P 2 2 { displaystyle P_ {2} ^ {2}} m ≤ ℓ, splňují podmínku ortogonality pro pevné m :
∫ − 1 1 P k m P ℓ m d X = 2 ( ℓ + m ) ! ( 2 ℓ + 1 ) ( ℓ − m ) ! δ k , ℓ { displaystyle int _ {- 1} ^ {1} P_ {k} ^ {m} P _ { ell} ^ {m} dx = { frac {2 ( ell + m)!} {(2 ell +1) ( ell -m)!}} delta _ {k, ell}} Kde δk , ℓKroneckerova delta .
Také splňují podmínku ortogonality pro fixní ℓ:
∫ − 1 1 P ℓ m P ℓ n 1 − X 2 d X = { 0 -li m ≠ n ( ℓ + m ) ! m ( ℓ − m ) ! -li m = n ≠ 0 ∞ -li m = n = 0 { displaystyle int _ {- 1} ^ {1} { frac {P _ { ell} ^ {m} P _ { ell} ^ {n}} {1-x ^ {2}}} dx = { begin {cases} 0 & { mbox {if}} m neq n { frac {( ell + m)!} {m ( ell -m)!}} & { mbox {if}} m = n neq 0 infty & { mbox {if}} m = n = 0 end {cases}}} Negativní m a / nebo negativní ℓ Diferenciální rovnice je při změně znaménka jasně neměnná m .
Funkce pro negativní m výše se ukázalo, že jsou úměrné těm pozitivním m :
P ℓ − m = ( − 1 ) m ( ℓ − m ) ! ( ℓ + m ) ! P ℓ m { displaystyle P _ { ell} ^ {- m} = (- 1) ^ {m} { frac {( ell -m)!} {( ell + m)!}} P _ { ell} ^ {m}} (Vyplývalo to z Rodriguesovy definice vzorce. Tato definice také umožňuje, aby různé vzorce opakování fungovaly jako pozitivní nebo negativní m .)
Li ∣ m ∣ > ℓ t h E n P ℓ m = 0. { displaystyle { textrm {If}} quad { mid} m { mid}> ell , quad mathrm {then} quad P _ { ell} ^ {m} = 0. ,}
Diferenciální rovnice je také neměnná při změně z ℓ na − ℓ - 1 a funkce pro záporné ℓ jsou definovány
P − ℓ m = P ℓ − 1 m , ( ℓ = 1 , 2 , . . . ) { displaystyle P _ {- ell} ^ {m} = P _ { ell -1} ^ {m}, ( ell = 1, , 2, , ...)} Parita Z jejich definice lze ověřit, že funkce Associated Legendre jsou sudé nebo liché podle
P ℓ m ( − X ) = ( − 1 ) ℓ + m P ℓ m ( X ) { displaystyle P _ { ell} ^ {m} (- x) = (- 1) ^ { ell + m} P _ { ell} ^ {m} (x)} Prvních pár přidružených funkcí Legendre Přidružené funkce Legendre pro m = 0
Přidružené funkce Legendre pro m = 1
Přidružené funkce Legendre pro m = 2
Prvních pár přidružených funkcí Legendre, včetně těch pro záporné hodnoty m , jsou:
P 0 0 ( X ) = 1 { displaystyle P_ {0} ^ {0} (x) = 1} P 1 − 1 ( X ) = − 1 2 P 1 1 ( X ) { displaystyle P_ {1} ^ {- 1} (x) = - { begin {matrix} { frac {1} {2}} end {matrix}} P_ {1} ^ {1} (x) } P 1 0 ( X ) = X { displaystyle P_ {1} ^ {0} (x) = x} P 1 1 ( X ) = − ( 1 − X 2 ) 1 / 2 { displaystyle P_ {1} ^ {1} (x) = - (1-x ^ {2}) ^ {1/2}} P 2 − 2 ( X ) = 1 24 P 2 2 ( X ) { displaystyle P_ {2} ^ {- 2} (x) = { begin {matrix} { frac {1} {24}} end {matrix}} P_ {2} ^ {2} (x)} P 2 − 1 ( X ) = − 1 6 P 2 1 ( X ) { displaystyle P_ {2} ^ {- 1} (x) = - { begin {matrix} { frac {1} {6}} end {matrix}} P_ {2} ^ {1} (x) } P 2 0 ( X ) = 1 2 ( 3 X 2 − 1 ) { displaystyle P_ {2} ^ {0} (x) = { begin {matrix} { frac {1} {2}} end {matrix}} (3x ^ {2} -1)} P 2 1 ( X ) = − 3 X ( 1 − X 2 ) 1 / 2 { displaystyle P_ {2} ^ {1} (x) = - 3x (1-x ^ {2}) ^ {1/2}} P 2 2 ( X ) = 3 ( 1 − X 2 ) { displaystyle P_ {2} ^ {2} (x) = 3 (1-x ^ {2})} P 3 − 3 ( X ) = − 1 720 P 3 3 ( X ) { displaystyle P_ {3} ^ {- 3} (x) = - { begin {matrix} { frac {1} {720}} end {matrix}} P_ {3} ^ {3} (x) } P 3 − 2 ( X ) = 1 120 P 3 2 ( X ) { displaystyle P_ {3} ^ {- 2} (x) = { begin {matrix} { frac {1} {120}} end {matrix}} P_ {3} ^ {2} (x)} P 3 − 1 ( X ) = − 1 12 P 3 1 ( X ) { displaystyle P_ {3} ^ {- 1} (x) = - { begin {matrix} { frac {1} {12}} end {matrix}} P_ {3} ^ {1} (x) } P 3 0 ( X ) = 1 2 ( 5 X 3 − 3 X ) { displaystyle P_ {3} ^ {0} (x) = { begin {matrix} { frac {1} {2}} end {matrix}} (5x ^ {3} -3x)} P 3 1 ( X ) = − 3 2 ( 5 X 2 − 1 ) ( 1 − X 2 ) 1 / 2 { displaystyle P_ {3} ^ {1} (x) = - { begin {matrix} { frac {3} {2}} end {matrix}} (5x ^ {2} -1) (1- x ^ {2}) ^ {1/2}} P 3 2 ( X ) = 15 X ( 1 − X 2 ) { displaystyle P_ {3} ^ {2} (x) = 15x (1-x ^ {2})} P 3 3 ( X ) = − 15 ( 1 − X 2 ) 3 / 2 { displaystyle P_ {3} ^ {3} (x) = - 15 (1-x ^ {2}) ^ {3/2}} P 4 − 4 ( X ) = 1 40320 P 4 4 ( X ) { displaystyle P_ {4} ^ {- 4} (x) = { begin {matrix} { frac {1} {40320}} end {matrix}} P_ {4} ^ {4} (x)} P 4 − 3 ( X ) = − 1 5040 P 4 3 ( X ) { displaystyle P_ {4} ^ {- 3} (x) = - { begin {matrix} { frac {1} {5040}} end {matrix}} P_ {4} ^ {3} (x) } P 4 − 2 ( X ) = 1 360 P 4 2 ( X ) { displaystyle P_ {4} ^ {- 2} (x) = { begin {matrix} { frac {1} {360}} end {matrix}} P_ {4} ^ {2} (x)} P 4 − 1 ( X ) = − 1 20 P 4 1 ( X ) { displaystyle P_ {4} ^ {- 1} (x) = - { begin {matrix} { frac {1} {20}} end {matrix}} P_ {4} ^ {1} (x) } P 4 0 ( X ) = 1 8 ( 35 X 4 − 30 X 2 + 3 ) { displaystyle P_ {4} ^ {0} (x) = { begin {matrix} { frac {1} {8}} end {matrix}} (35x ^ {4} -30x ^ {2} + 3)} P 4 1 ( X ) = − 5 2 ( 7 X 3 − 3 X ) ( 1 − X 2 ) 1 / 2 { displaystyle P_ {4} ^ {1} (x) = - { begin {matrix} { frac {5} {2}} end {matrix}} (7x ^ {3} -3x) (1- x ^ {2}) ^ {1/2}} P 4 2 ( X ) = 15 2 ( 7 X 2 − 1 ) ( 1 − X 2 ) { displaystyle P_ {4} ^ {2} (x) = { begin {matrix} { frac {15} {2}} end {matrix}} (7x ^ {2} -1) (1-x ^ {2})} P 4 3 ( X ) = − 105 X ( 1 − X 2 ) 3 / 2 { displaystyle P_ {4} ^ {3} (x) = - 105x (1-x ^ {2}) ^ {3/2}} P 4 4 ( X ) = 105 ( 1 − X 2 ) 2 { displaystyle P_ {4} ^ {4} (x) = 105 (1-x ^ {2}) ^ {2}} Vzorec opakování Tyto funkce mají řadu vlastností opakování:
( ℓ − m + 1 ) P ℓ + 1 m ( X ) = ( 2 ℓ + 1 ) X P ℓ m ( X ) − ( ℓ + m ) P ℓ − 1 m ( X ) { displaystyle ( ell -m + 1) P _ { ell +1} ^ {m} (x) = (2 ell +1) xP _ { ell} ^ {m} (x) - ( ell + m) P _ { ell -1} ^ {m} (x)} 2 m X P ℓ m ( X ) = − 1 − X 2 [ P ℓ m + 1 ( X ) + ( ℓ + m ) ( ℓ − m + 1 ) P ℓ m − 1 ( X ) ] { displaystyle 2mxP _ { ell} ^ {m} (x) = - { sqrt {1-x ^ {2}}} vlevo [P _ { ell} ^ {m + 1} (x) + ( ell + m) ( ell -m + 1) P _ { ell} ^ {m-1} (x) right]} 1 1 − X 2 P ℓ m ( X ) = − 1 2 m [ P ℓ − 1 m + 1 ( X ) + ( ℓ + m − 1 ) ( ℓ + m ) P ℓ − 1 m − 1 ( X ) ] { displaystyle { frac {1} { sqrt {1-x ^ {2}}}} P _ { ell} ^ {m} (x) = { frac {-1} {2m}} vlevo [ P _ { ell -1} ^ {m + 1} (x) + ( ell + m-1) ( ell + m) P _ { ell -1} ^ {m-1} (x) vpravo] } 1 1 − X 2 P ℓ m ( X ) = − 1 2 m [ P ℓ + 1 m + 1 ( X ) + ( ℓ − m + 1 ) ( ℓ − m + 2 ) P ℓ + 1 m − 1 ( X ) ] { displaystyle { frac {1} { sqrt {1-x ^ {2}}}} P _ { ell} ^ {m} (x) = { frac {-1} {2m}} vlevo [ P _ { ell +1} ^ {m + 1} (x) + ( ell -m + 1) ( ell -m + 2) P _ { ell +1} ^ {m-1} (x) že jo]} 1 − X 2 P ℓ m ( X ) = 1 2 ℓ + 1 [ ( ℓ − m + 1 ) ( ℓ − m + 2 ) P ℓ + 1 m − 1 ( X ) − ( ℓ + m − 1 ) ( ℓ + m ) P ℓ − 1 m − 1 ( X ) ] { displaystyle { sqrt {1-x ^ {2}}} P _ { ell} ^ {m} (x) = { frac {1} {2 ell +1}} left [( ell - m + 1) ( ell -m + 2) P _ { ell +1} ^ {m-1} (x) - ( ell + m-1) ( ell + m) P _ { ell -1} ^ {m-1} (x) vpravo]} 1 − X 2 P ℓ m ( X ) = − 1 2 ℓ + 1 [ P ℓ + 1 m + 1 ( X ) − P ℓ − 1 m + 1 ( X ) ] { displaystyle { sqrt {1-x ^ {2}}} P _ { ell} ^ {m} (x) = { frac {-1} {2 ell +1}} left [P _ { ell +1} ^ {m + 1} (x) -P _ { ell -1} ^ {m + 1} (x) right]} 1 − X 2 P ℓ m + 1 ( X ) = ( ℓ − m ) X P ℓ m ( X ) − ( ℓ + m ) P ℓ − 1 m ( X ) { displaystyle { sqrt {1-x ^ {2}}} P _ { ell} ^ {m + 1} (x) = ( ell -m) xP _ { ell} ^ {m} (x) - ( ell + m) P _ { ell -1} ^ {m} (x)} 1 − X 2 P ℓ m + 1 ( X ) = ( ℓ − m + 1 ) P ℓ + 1 m ( X ) − ( ℓ + m + 1 ) X P ℓ m ( X ) { displaystyle { sqrt {1-x ^ {2}}} P _ { ell} ^ {m + 1} (x) = ( ell -m + 1) P _ { ell +1} ^ {m} (x) - ( ell + m + 1) xP _ { ell} ^ {m} (x)} 1 − X 2 d d X P ℓ m ( X ) = 1 2 [ ( ℓ + m ) ( ℓ − m + 1 ) P ℓ m − 1 ( X ) − P ℓ m + 1 ( X ) ] { displaystyle { sqrt {1-x ^ {2}}} { frac {d} {dx}} {P _ { ell} ^ {m}} (x) = { frac {1} {2} } left [( ell + m) ( ell -m + 1) P _ { ell} ^ {m-1} (x) -P _ { ell} ^ {m + 1} (x) right) } ( 1 − X 2 ) d d X P ℓ m ( X ) = 1 2 ℓ + 1 [ ( ℓ + 1 ) ( ℓ + m ) P ℓ − 1 m ( X ) − ℓ ( ℓ − m + 1 ) P ℓ + 1 m ( X ) ] { displaystyle (1-x ^ {2}) { frac {d} {dx}} {P _ { ell} ^ {m}} (x) = { frac {1} {2 ell +1} } left [( ell +1) ( ell + m) P _ { ell -1} ^ {m} (x) - ell ( ell -m + 1) P _ { ell +1} ^ { m} (x) vpravo]} ( X 2 − 1 ) d d X P ℓ m ( X ) = ℓ X P ℓ m ( X ) − ( ℓ + m ) P ℓ − 1 m ( X ) { displaystyle (x ^ {2} -1) { frac {d} {dx}} {P _ { ell} ^ {m}} (x) = { ell} xP _ { ell} ^ {m} (x) - ( ell + m) P _ { ell -1} ^ {m} (x)} ( X 2 − 1 ) d d X P ℓ m ( X ) = − ( ℓ + 1 ) X P ℓ m ( X ) + ( ℓ − m + 1 ) P ℓ + 1 m ( X ) { displaystyle (x ^ {2} -1) { frac {d} {dx}} {P _ { ell} ^ {m}} (x) = - ( ell +1) xP _ { ell} ^ {m} (x) + ( ell -m + 1) P _ { ell +1} ^ {m} (x)} ( X 2 − 1 ) d d X P ℓ m ( X ) = 1 − X 2 P ℓ m + 1 ( X ) + m X P ℓ m ( X ) { displaystyle (x ^ {2} -1) { frac {d} {dx}} {P _ { ell} ^ {m}} (x) = { sqrt {1-x ^ {2}}} P _ { ell} ^ {m + 1} (x) + mxP _ { ell} ^ {m} (x)} ( X 2 − 1 ) d d X P ℓ m ( X ) = − ( ℓ + m ) ( ℓ − m + 1 ) 1 − X 2 P ℓ m − 1 ( X ) − m X P ℓ m ( X ) { displaystyle (x ^ {2} -1) { frac {d} {dx}} {P _ { ell} ^ {m}} (x) = - ( ell + m) ( ell -m + 1) { sqrt {1-x ^ {2}}} P _ { ell} ^ {m-1} (x) -mxP _ { ell} ^ {m} (x)} Užitečné identity (počáteční hodnoty pro první rekurzi):
P ℓ + 1 ℓ + 1 ( X ) = − ( 2 ℓ + 1 ) 1 − X 2 P ℓ ℓ ( X ) { displaystyle P _ { ell +1} ^ { ell +1} (x) = - (2 ell +1) { sqrt {1-x ^ {2}}} P _ { ell} ^ { ell} (x)} P ℓ ℓ ( X ) = ( − 1 ) ℓ ( 2 ℓ − 1 ) ! ! ( 1 − X 2 ) ( ℓ / 2 ) { displaystyle P _ { ell} ^ { ell} (x) = (- 1) ^ { ell} (2 ell -1) !! (1-x ^ {2}) ^ {( ell / 2)}} P ℓ + 1 ℓ ( X ) = X ( 2 ℓ + 1 ) P ℓ ℓ ( X ) { displaystyle P _ { ell +1} ^ { ell} (x) = x (2 ell +1) P _ { ell} ^ { ell} (x)} s !! the dvojitý faktoriál .
Gauntův vzorec Integrál nad produktem tří přidružených Legendrových polynomů (s odpovídajícími objednávkami, jak je uvedeno níže) je nezbytnou přísadou při vývoji produktů Legendrových polynomů do řady lineární v Legendrových polynomech. Ukázalo se to například jako nezbytné při provádění atomových výpočtů Hartree – Fock odrůda, kde jsou potřeba maticové prvky operátora Coulomb. K tomu máme Gauntův vzorec [3]
1 2 ∫ − 1 1 P l u ( X ) P m proti ( X ) P n w ( X ) d X = { displaystyle { frac {1} {2}} int _ {- 1} ^ {1} P_ {l} ^ {u} (x) P_ {m} ^ {v} (x) P_ {n} ^ {w} (x) dx =} ( − 1 ) s − m − w ( m + proti ) ! ( n + w ) ! ( 2 s − 2 n ) ! s ! ( m − proti ) ! ( s − l ) ! ( s − m ) ! ( s − n ) ! ( 2 s + 1 ) ! { displaystyle (-1) ^ {smw} { frac {(m + v)! (n + w)! (2s-2n)! s!} {(mv)! (sl)! (sm)! ( sn)! (2s + 1)!}}} × ∑ t = str q ( − 1 ) t ( l + u + t ) ! ( m + n − u − t ) ! t ! ( l − u − t ) ! ( m − n + u + t ) ! ( n − w − t ) ! { displaystyle times sum _ {t = p} ^ {q} (- 1) ^ {t} { frac {(l + u + t)! (m + matice)!} {t! (lut )! (m-n + u + t)! (nwt)!}}}
Tento vzorec se použije za následujících předpokladů:
stupně jsou nezáporná celá čísla l , m , n ≥ 0 { displaystyle l, m, n geq 0} všechny tři objednávky jsou nezáporná celá čísla u , proti , w ≥ 0 { displaystyle u, proti, w geq 0} u { displaystyle u} objednávky sečtou u = proti + w { displaystyle u = v + w} stupně poslouchají m ≥ n { displaystyle m geq n} Další množství, která se objevují ve vzorci, jsou definována jako
2 s = l + m + n { displaystyle 2s = l + m + n} str = max ( 0 , n − m − u ) { displaystyle p = max (0, , n-m-u)} q = min ( m + n − u , l − u , n − w ) { displaystyle q = min (m + n-u, , l-u, , n-w)} Integrál je nula, pokud
součet stupňů je dokonce tak, že s { displaystyle s} trojúhelníková podmínka je splněna m + n ≥ l ≥ m − n { displaystyle m + n geq l geq m-n} Dong a Lemus (2002)[4]
Zobecnění pomocí hypergeometrických funkcí Tyto funkce mohou být ve skutečnosti definovány pro obecné komplexní parametry a argumenty:
P λ μ ( z ) = 1 Γ ( 1 − μ ) [ 1 + z 1 − z ] μ / 2 2 F 1 ( − λ , λ + 1 ; 1 − μ ; 1 − z 2 ) { displaystyle P _ { lambda} ^ { mu} (z) = { frac {1} { Gamma (1- mu)}} vlevo [{ frac {1 + z} {1-z} } right] ^ { mu / 2} , _ {2} F_ {1} (- lambda, lambda +1; 1- mu; { frac {1-z} {2}})} kde Γ { displaystyle Gamma} funkce gama a 2 F 1 { displaystyle _ {2} F_ {1}} hypergeometrická funkce
2 F 1 ( α , β ; y ; z ) = Γ ( y ) Γ ( α ) Γ ( β ) ∑ n = 0 ∞ Γ ( n + α ) Γ ( n + β ) Γ ( n + y ) n ! z n , { displaystyle , _ {2} F_ {1} ( alfa, beta; gama; z) = { frac { gama ( gama)} { gama ( alfa) gama ( beta) }} sum _ {n = 0} ^ { infty} { frac { Gamma (n + alpha) Gamma (n + beta)} { Gamma (n + gamma) n!}} z ^ { n},} Říká se jim Legendární funkce pokud jsou definovány tímto obecnějším způsobem. Splňují stejnou diferenciální rovnici jako dříve:
( 1 − z 2 ) y ″ − 2 z y ′ + ( λ [ λ + 1 ] − μ 2 1 − z 2 ) y = 0. { displaystyle (1-z ^ {2}) , y '' - 2zy '+ vlevo ( lambda [ lambda +1] - { frac { mu ^ {2}} {1-z ^ { 2}}} vpravo) , y = 0. ,} Jelikož se jedná o diferenciální rovnici druhého řádu, má druhé řešení, Q λ μ ( z ) { displaystyle Q _ { lambda} ^ { mu} (z)}
Q λ μ ( z ) = π Γ ( λ + μ + 1 ) 2 λ + 1 Γ ( λ + 3 / 2 ) 1 z λ + μ + 1 ( 1 − z 2 ) μ / 2 2 F 1 ( λ + μ + 1 2 , λ + μ + 2 2 ; λ + 3 2 ; 1 z 2 ) { displaystyle Q _ { lambda} ^ { mu} (z) = { frac {{ sqrt { pi}} gama ( lambda + mu +1)} {2 ^ { lambda +1 } Gamma ( lambda +3/2)}} { frac {1} {z ^ { lambda + mu +1}}} (1-z ^ {2}) ^ { mu / 2} , _ {2} F_ {1} left ({ frac { lambda + mu +1} {2}}, { frac { lambda + mu +2} {2}}; lambda + { frac {3} {2}}; { frac {1} {z ^ {2}}} vpravo)} P λ μ ( z ) { displaystyle P _ { lambda} ^ { mu} (z)} Q λ μ ( z ) { displaystyle Q _ { lambda} ^ { mu} (z)}
Reparameterizace z hlediska úhlů Tyto funkce jsou nejužitečnější, když je argument přeparametrizován z hlediska úhlů, nechat X = cos θ { displaystyle x = cos theta}
P ℓ m ( cos θ ) = ( − 1 ) m ( hřích θ ) m d m d ( cos θ ) m ( P ℓ ( cos θ ) ) { displaystyle P _ { ell} ^ {m} ( cos theta) = (- 1) ^ {m} ( sin theta) ^ {m} { frac {d ^ {m}} {d ( cos theta) ^ {m}}} vlevo (P _ { ell} ( cos theta) vpravo) ,} Použití relace ( 1 − X 2 ) 1 / 2 = hřích θ { displaystyle (1-x ^ {2}) ^ {1/2} = sin theta} výše uvedený seznam získá prvních několik polynomů, parametrizovaných tímto způsobem, jako:
P 0 0 ( cos θ ) = 1 P 1 0 ( cos θ ) = cos θ P 1 1 ( cos θ ) = − hřích θ P 2 0 ( cos θ ) = 1 2 ( 3 cos 2 θ − 1 ) P 2 1 ( cos θ ) = − 3 cos θ hřích θ P 2 2 ( cos θ ) = 3 hřích 2 θ P 3 0 ( cos θ ) = 1 2 ( 5 cos 3 θ − 3 cos θ ) P 3 1 ( cos θ ) = − 3 2 ( 5 cos 2 θ − 1 ) hřích θ P 3 2 ( cos θ ) = 15 cos θ hřích 2 θ P 3 3 ( cos θ ) = − 15 hřích 3 θ P 4 0 ( cos θ ) = 1 8 ( 35 cos 4 θ − 30 cos 2 θ + 3 ) P 4 1 ( cos θ ) = − 5 2 ( 7 cos 3 θ − 3 cos θ ) hřích θ P 4 2 ( cos θ ) = 15 2 ( 7 cos 2 θ − 1 ) hřích 2 θ P 4 3 ( cos θ ) = − 105 cos θ hřích 3 θ P 4 4 ( cos θ ) = 105 hřích 4 θ { displaystyle { begin {zarovnaný} P_ {0} ^ {0} ( cos theta) & = 1 [8pt] P_ {1} ^ {0} ( cos theta) & = cos theta [8pt] P_ {1} ^ {1} ( cos theta) & = - sin theta [8pt] P_ {2} ^ {0} ( cos theta) & = { tfrac {1} {2}} (3 cos ^ {2} theta -1) [8pt] P_ {2} ^ {1} ( cos theta) & = - 3 cos theta sin theta [8pt] P_ {2} ^ {2} ( cos theta) & = 3 sin ^ {2} theta [8pt] P_ {3} ^ {0} ( cos theta ) & = { tfrac {1} {2}} (5 cos ^ {3} theta -3 cos theta) [8pt] P_ {3} ^ {1} ( cos theta) & = - { tfrac {3} {2}} (5 cos ^ {2} theta -1) sin theta [8pt] P_ {3} ^ {2} ( cos theta) & = 15 cos theta sin ^ {2} theta [8pt] P_ {3} ^ {3} ( cos theta) & = - 15 sin ^ {3} theta [8pt] P_ {4} ^ {0} ( cos theta) & = { tfrac {1} {8}} (35 cos ^ {4} theta -30 cos ^ {2} theta +3) [8pt] P_ {4} ^ {1} ( cos theta) & = - { tfrac {5} {2}} (7 cos ^ {3} theta -3 cos theta) sin theta [8pt] P_ {4} ^ {2} ( cos theta) & = { tfrac {15} {2}} (7 cos ^ {2} theta -1) sin ^ {2 } theta [8pt] P_ {4} ^ {3} ( cos theta) & = - 105 cos theta sin ^ {3} theta [8pt] P_ {4} ^ {4 } ( cos theta) & = 105 sin ^ {4} theta end {zarovnáno}}} Vztahy ortogonality uvedené výše se stávají v této formulaci: pro pevné m , P ℓ m ( cos θ ) { displaystyle P _ { ell} ^ {m} ( cos theta)} [ 0 , π ] { displaystyle [0, pi]} hřích θ { displaystyle sin theta}
∫ 0 π P k m ( cos θ ) P ℓ m ( cos θ ) hřích θ d θ = 2 ( ℓ + m ) ! ( 2 ℓ + 1 ) ( ℓ − m ) ! δ k , ℓ { displaystyle int _ {0} ^ { pi} P_ {k} ^ {m} ( cos theta) P _ { ell} ^ {m} ( cos theta) , sin theta , d theta = { frac {2 ( ell + m)!} {(2 ell +1) ( ell -m)!}} delta _ {k, ell}} Také pro pevné ℓ:
∫ 0 π P ℓ m ( cos θ ) P ℓ n ( cos θ ) csc θ d θ = { 0 -li m ≠ n ( ℓ + m ) ! m ( ℓ − m ) ! -li m = n ≠ 0 ∞ -li m = n = 0 { displaystyle int _ {0} ^ { pi} P _ { ell} ^ {m} ( cos theta) P _ { ell} ^ {n} ( cos theta) csc theta , d theta = { begin {cases} 0 & { text {if}} m neq n { frac {( ell + m)!} {m ( ell -m)!}} & { text {if}} m = n neq 0 infty & { text {if}} m = n = 0 end {cases}}} Pokud jde o θ, P ℓ m ( cos θ ) { displaystyle P _ { ell} ^ {m} ( cos theta)}
d 2 y d θ 2 + dětská postýlka θ d y d θ + [ λ − m 2 hřích 2 θ ] y = 0 { displaystyle { frac {d ^ {2} y} {d theta ^ {2}}} + cot theta { frac {dy} {d theta}} + left [ lambda - { frac {m ^ {2}} { sin ^ {2} theta}} vpravo] , y = 0 ,} Přesněji řečeno, dané celé číslo m ≥ { displaystyle geq} λ = ℓ ( ℓ + 1 ) { displaystyle lambda = ell ( ell +1) ,} m a tato řešení jsou přiměřená P ℓ m ( cos θ ) { displaystyle P _ { ell} ^ {m} ( cos theta)}
Aplikace ve fyzice: sférické harmonické Při mnoha příležitostech v fyzika , kde se vyskytují související legendární polynomy z hlediska úhlů sférický symetrie je zapojen. Úhel souměrnosti v sférické souřadnice je úhel θ { displaystyle theta} ϕ { displaystyle phi} sférické harmonické . Tyto funkce vyjadřují symetrii dvě koule v rámci akce Lež skupina SO (3).
Tyto funkce jsou užitečné proto, že jsou ústředním bodem řešení rovnice ∇ 2 ψ + λ ψ = 0 { displaystyle nabla ^ {2} psi + lambda psi = 0} Laplacian je
∇ 2 ψ = ∂ 2 ψ ∂ θ 2 + dětská postýlka θ ∂ ψ ∂ θ + csc 2 θ ∂ 2 ψ ∂ ϕ 2 . { displaystyle nabla ^ {2} psi = { frac { částečné ^ {2} psi} { částečné theta ^ {2}}} + cot theta { frac { částečné psi} { částečné theta}} + csc ^ {2} theta { frac { částečné ^ {2} psi} { částečné phi ^ {2}}}.} Když parciální diferenciální rovnice
∂ 2 ψ ∂ θ 2 + dětská postýlka θ ∂ ψ ∂ θ + csc 2 θ ∂ 2 ψ ∂ ϕ 2 + λ ψ = 0 { displaystyle { frac { částečné ^ {2} psi} { částečné theta ^ {2}}} + cot theta { frac { částečné psi} { částečné theta}} + csc ^ {2} theta { frac { částečné ^ {2} psi} { částečné phi ^ {2}}} + lambda psi = 0} je řešena metodou oddělení proměnných , jeden dostane část závislou na φ hřích ( m ϕ ) { displaystyle sin (m phi)} cos ( m ϕ ) { displaystyle cos (m phi)}
d 2 y d θ 2 + dětská postýlka θ d y d θ + [ λ − m 2 hřích 2 θ ] y = 0 { displaystyle { frac {d ^ {2} y} {d theta ^ {2}}} + cot theta { frac {dy} {d theta}} + left [ lambda - { frac {m ^ {2}} { sin ^ {2} theta}} vpravo] , y = 0 ,} pro které jsou řešení P ℓ m ( cos θ ) { displaystyle P _ { ell} ^ {m} ( cos theta)} ℓ ≥ m { displaystyle ell { geq} m} λ = ℓ ( ℓ + 1 ) { displaystyle lambda = ell ( ell +1)}
Proto rovnice
∇ 2 ψ + λ ψ = 0 { displaystyle nabla ^ {2} psi + lambda psi = 0} má nesingulární oddělená řešení, pouze když λ = ℓ ( ℓ + 1 ) { displaystyle lambda = ell ( ell +1)}
P ℓ m ( cos θ ) cos ( m ϕ ) 0 ≤ m ≤ ℓ { Displaystyle P _ { ell} ^ {m} ( cos theta) cos (m phi) 0 leq m leq ell} a
P ℓ m ( cos θ ) hřích ( m ϕ ) 0 < m ≤ ℓ . { Displaystyle P _ { ell} ^ {m} ( cos theta) sin (m phi) 0 Pro každou volbu ℓ existují 2ℓ + 1 funkce pro různé hodnoty m a volby sinu a kosinu. Všechny jsou ortogonální v obou ℓ a m pokud jsou integrovány přes povrch koule.
Řešení jsou obvykle psána ve smyslu komplexní exponenciály :
Y ℓ , m ( θ , ϕ ) = ( 2 ℓ + 1 ) ( ℓ − m ) ! 4 π ( ℓ + m ) ! P ℓ m ( cos θ ) E i m ϕ − ℓ ≤ m ≤ ℓ . { displaystyle Y _ { ell, m} ( theta, phi) = { sqrt { frac {(2 ell +1) ( ell -m)!} {4 pi ( ell + m) !}}} P _ { ell} ^ {m} ( cos theta) e ^ {im phi} qquad - ell leq m leq ell.} Funkce Y ℓ , m ( θ , ϕ ) { displaystyle Y _ { ell, m} ( theta, phi)} sférické harmonické a množství v druhé odmocnině je normalizační faktor. Připomínáme vztah mezi přidruženými Legendrovými funkcemi kladné a záporné m , je snadno prokázáno, že sférické harmonické uspokojují identitu[5]
Y ℓ , m ∗ ( θ , ϕ ) = ( − 1 ) m Y ℓ , − m ( θ , ϕ ) . { displaystyle Y _ { ell, m} ^ {*} ( theta, phi) = (- 1) ^ {m} Y _ { ell, -m} ( theta, phi).} Sférické harmonické funkce tvoří úplnou ortonormální sadu funkcí ve smyslu Fourierova řada . Pracovníci v oborech geodézie, geomagnetismu a spektrální analýzy používají jinou fázi a normalizační faktor, než jsou zde uvedeny (viz sférické harmonické ).
Když je trojrozměrná sféricky symetrická parciální diferenciální rovnice řešena metodou separace proměnných ve sférických souřadnicích, část, která zůstane po odstranění radiální části, je obvykle ve formě
∇ 2 ψ ( θ , ϕ ) + λ ψ ( θ , ϕ ) = 0 , { displaystyle nabla ^ {2} psi ( theta, phi) + lambda psi ( theta, phi) = 0,} a proto jsou řešení sférické harmonické.
Zobecnění Legendrovy polynomy úzce souvisí hypergeometrická řada . Ve formě sférických harmonických vyjadřují symetrii dvě koule v rámci akce Lež skupina SO (3). Kromě SO (3) existuje mnoho dalších Lieových skupin a existuje analogické zobecnění Legendrových polynomů, které vyjadřují symetrie polojednodušých Lieových skupin a Riemannovy symetrické prostory . V hrubém smyslu lze definovat a Laplacian na symetrických prostorech; vlastní funkce Laplacian lze považovat za zobecnění sférických harmonických pro jiná nastavení.
Viz také Poznámky a odkazy ^ Courant & Hilbert 1953 , V, §10.^ Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [červen 1964]. „Kapitola 8“ . Příručka matematických funkcí se vzorci, grafy a matematickými tabulkami 55 (Devátý dotisk s dalšími opravami desátého originálu s opravami (prosinec 1972); první vydání.). Washington DC.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. str. 332. ISBN 978-0-486-61272-0 LCCN 64-60036 . PAN 0167642 . LCCN 65-12253 .^ Od Johna C. Slatera Kvantová teorie atomové struktury , McGraw-Hill (New York, 1960), svazek I, strana 309, který cituje původní práci J. A. Gaunta, Filozofické transakce Královské společnosti v Londýně , A228: 151 (1929) ^ Dong S.H., Lemus R., (2002), "Překrývající se integrál tří přidružených Legendrových polynomů" , Appl. Matematika. Lett. 15, 541-546. ^ Tuto identitu lze také ukázat vztahem sférických harmonických k Wigner D-matice a použití jeho vlastnosti obrácení času. Vztah mezi souvisejícími Legendrovými funkcemi ±m lze pak dokázat ze složité konjugační identity sférických harmonických. Arfken, G.B .; Weber, H.J. (2001), Matematické metody pro fyziky Akademický tisk, ISBN 978-0-12-059825-0 Belousov, S.L. (1962), Tabulky normalizovaných asociovaných legendárních polynomů , Matematické tabulky, 18 , Pergamon Press Condon, E. U .; Shortley, G. H. (1970), Teorie atomového spektra , Cambridge, Anglie: Cambridge University Press, OCLC 5388084 Courant, Richarde ; Hilbert, David (1953), Metody matematické fyziky, svazek 1 , New York: Interscience Publischer, Inc.Dunster, T. M. (2010), „Legendre a související funkce“ , v Olver, Frank W. J. ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 PAN 2723248 Edmonds, A.R. (1957), Moment hybnosti v kvantové mechanice ISBN 978-0-691-07912-7 Hildebrand, F. B. (1976), Pokročilý počet pro aplikace , Prentice Hall, ISBN 978-0-13-011189-0 Koornwinder, Tom H .; Wong, Roderick S. C .; Koekoek, Roelof; Swarttouw, René F. (2010), „Ortogonální polynomy“ , v Olver, Frank W. J. ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 PAN 2723248 Schach, S.R. (1973) Nové identity pro funkce spojené s legendou integrovaného řádu a stupně externí odkazy 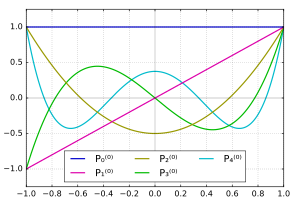



![(1-x ^ {2}) { frac {d ^ {2}} {dx ^ {2}}} P _ { ell} ^ {m} (x) -2x { frac {d} {dx} } P _ { ell} ^ {m} (x) + left [ ell ( ell +1) - { frac {m ^ {2}} {1-x ^ {2}}} vpravo] P_ { ell} ^ {m} (x) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d8e4b95ac4a81fd84aa2768d8f6381ca74fabf)
![{ frac {d} {dx}} left [(1-x ^ {2}) { frac {d} {dx}} P _ { ell} ^ {m} (x) right] + left [ ell ( ell +1) - { frac {m ^ {2}} {1-x ^ {2}}} right] P _ { ell} ^ {m} (x) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/918ec803eebef3f5df089511e301ce99f1695395)



![P _ { ell} (x) = { frac {1} {2 ^ { ell} , ell!}} { Frac {d ^ { ell}} {dx ^ { ell}}} left [(x ^ {2} -1) ^ { ell} right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ca96dae138d4dc21c8eb5ee22e0f3c09d8b2ae)








































![2mxP _ { ell} ^ {m} (x) = - { sqrt {1-x ^ {2}}} left [P _ { ell} ^ {m + 1} (x) + ( ell + m ) ( ell -m + 1) P _ { ell} ^ {m-1} (x) vpravo]](https://wikimedia.org/api/rest_v1/media/math/render/svg/16b8c51959e61b723fca74ad217ca195809a70d1)
![{ frac {1} { sqrt {1-x ^ {2}}}} P _ { ell} ^ {m} (x) = { frac {-1} {2m}} left [P _ { ell -1} ^ {m + 1} (x) + ( ell + m-1) ( ell + m) P _ { ell -1} ^ {m-1} (x) right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e697003e6ca8eba77eafc0ee9584a1bb0f73b97a)
![{ frac {1} { sqrt {1-x ^ {2}}}} P _ { ell} ^ {m} (x) = { frac {-1} {2m}} left [P _ { ell +1} ^ {m + 1} (x) + ( ell -m + 1) ( ell -m + 2) P _ { ell +1} ^ {m-1} (x) right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a85ac33b2bfe757e1c5680ce2bcb075febcb0258)
![{ sqrt {1-x ^ {2}}} P _ { ell} ^ {m} (x) = { frac {1} {2 ell +1}} left [( ell -m + 1 ) ( ell -m + 2) P _ { ell +1} ^ {m-1} (x) - ( ell + m-1) ( ell + m) P _ { ell -1} ^ {m -1} (x) vpravo]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa0b88f261e938f80c8b93576b8bf3e290727722)
![{ displaystyle { sqrt {1-x ^ {2}}} P _ { ell} ^ {m} (x) = { frac {-1} {2 ell +1}} left [P _ { ell +1} ^ {m + 1} (x) -P _ { ell -1} ^ {m + 1} (x) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a962cf8ad9bbf80839d79f5f0afe89ef6d2c741)



![(1-x ^ {2}) { frac {d} {dx}} {P _ { ell} ^ {m}} (x) = { frac {1} {2 ell +1}} vlevo [( ell +1) ( ell + m) P _ { ell -1} ^ {m} (x) - ell ( ell -m + 1) P _ { ell +1} ^ {m} ( x) vpravo]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c189752c02a82355c76baf09259946997196d2a)




















![P _ { lambda} ^ { mu} (z) = { frac {1} { Gamma (1- mu)}} left [{ frac {1 + z} {1-z}} right ] ^ { mu / 2} , _ {2} F_ {1} (- lambda, lambda +1; 1- mu; { frac {1-z} {2}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/a33abd8dbaad6ee01cef4e0d064a2ebd78aad53a)



![(1-z ^ {2}) , y '' - 2zy '+ left ( lambda [ lambda +1] - { frac { mu ^ {2}} {1-z ^ {2}} } vpravo) , y = 0. ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/abfb2180fe5518a23933ad4fa6f8ed20bba11855)






![{ begin {aligned} P_ {0} ^ {0} ( cos theta) & = 1 [8pt] P_ {1} ^ {0} ( cos theta) & = cos theta [8pt] P_ {1} ^ {1} ( cos theta) & = - sin theta [8pt] P_ {2} ^ {0} ( cos theta) & = { tfrac {1 } {2}} (3 cos ^ {2} theta -1) [8pt] P_ {2} ^ {1} ( cos theta) & = - 3 cos theta sin theta [8pt] P_ {2} ^ {2} ( cos theta) & = 3 sin ^ {2} theta [8pt] P_ {3} ^ {0} ( cos theta) & = { tfrac {1} {2}} (5 cos ^ {3} theta -3 cos theta) [8pt] P_ {3} ^ {1} ( cos theta) & = - { tfrac {3} {2}} (5 cos ^ {2} theta -1) sin theta [8pt] P_ {3} ^ {2} ( cos theta) & = 15 cos theta sin ^ {2} theta [8pt] P_ {3} ^ {3} ( cos theta) & = - 15 sin ^ {3} theta [8pt] P_ {4} ^ {0} ( cos theta) & = { tfrac {1} {8}} (35 cos ^ {4} theta -30 cos ^ {2} theta +3) [8pt] P_ {4} ^ {1} ( cos theta) & = - { tfrac {5} {2}} (7 cos ^ {3} theta -3 cos theta) sin theta [8pt] P_ {4} ^ {2} ( cos theta) & = { tfrac {15} {2}} (7 cos ^ {2} theta -1) sin ^ {2} theta [8pt] P_ {4} ^ {3} ( cos theta) & = - 105 cos theta sin ^ {3} theta [8pt] P_ {4} ^ {4} ( cos theta) & = 105 sin ^ {4} theta end {zarovnáno}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ddaa2766fcd73e8e64234f1f511089d9e11f97d)

![[0, pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)



![{frac {d^{2}y}{d heta ^{2}}}+cot heta {frac {dy}{d heta }}+left[lambda -{frac {m^{2}}{sin ^{2} heta }}
ight],y=0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf734246861cd768b5d9f61be5f5f3b0f3f502f5)
















